This article begins a new series on linear algebra in Go, demonstrating how to perform numerical computations using the gonum library. If you’ve followed the Linear Algebra Crash Course in Python, this series provides a parallel implementation in Go with performance comparisons.
Linear Algebra: Golang Series - View all articles in this series.
Go offers advantages for linear algebra workloads: strong concurrency support, compile-time type checking, and excellent performance. The gonum ecosystem provides production-ready linear algebra, statistics, and plotting capabilities.
Setting Up Gonum
First, install the gonum packages:
go get gonum.org/v1/gonum/...
go get gonum.org/v1/plot/...
Import the necessary packages:
package main
import (
"fmt"
"math"
"gonum.org/v1/gonum/floats"
"gonum.org/v1/gonum/mat"
)
Creating Vectors
In gonum, vectors are represented using mat.VecDense:
package main
import (
"fmt"
"gonum.org/v1/gonum/mat"
)
func main() {
// Create a vector from a slice
data := []float64{1.0, 2.0, 3.0, 4.0}
v := mat.NewVecDense(len(data), data)
fmt.Printf("Vector v:\n%v\n", mat.Formatted(v))
fmt.Printf("Length: %d\n", v.Len())
// Access individual elements
fmt.Printf("v[0] = %.2f\n", v.AtVec(0))
fmt.Printf("v[2] = %.2f\n", v.AtVec(2))
}
Output:
Vector v:
[1]
[2]
[3]
[4]
Length: 4
v[0] = 1.00
v[2] = 3.00
Vector Operations
Addition and Subtraction
func vectorAddition() {
v1 := mat.NewVecDense(3, []float64{1, 2, 3})
v2 := mat.NewVecDense(3, []float64{4, 5, 6})
// Addition: result = v1 + v2
result := mat.NewVecDense(3, nil)
result.AddVec(v1, v2)
fmt.Printf("v1 + v2 = %v\n", mat.Formatted(result.T()))
// Subtraction: result = v1 - v2
result.SubVec(v1, v2)
fmt.Printf("v1 - v2 = %v\n", mat.Formatted(result.T()))
}
Output:
v1 + v2 = [5 7 9]
v1 - v2 = [-3 -3 -3]
Scalar Multiplication
func scalarMultiplication() {
v := mat.NewVecDense(3, []float64{1, 2, 3})
scalar := 2.5
// Scale the vector
result := mat.NewVecDense(3, nil)
result.ScaleVec(scalar, v)
fmt.Printf("%.1f * v = %v\n", scalar, mat.Formatted(result.T()))
}
Output:
2.5 * v = [2.5 5 7.5]
Dot Product
The dot product (inner product) of two vectors:
func dotProduct() {
v1 := mat.NewVecDense(4, []float64{1, 2, 3, 4})
v2 := mat.NewVecDense(4, []float64{2, 3, 4, 5})
// Dot product
dot := mat.Dot(v1, v2)
fmt.Printf("v1 · v2 = %.2f\n", dot)
// Manual calculation: 1*2 + 2*3 + 3*4 + 4*5 = 2 + 6 + 12 + 20 = 40
}
Output:
v1 · v2 = 40.00
Vector Norms
The norm (magnitude) of a vector measures its length:
import "gonum.org/v1/gonum/floats"
func vectorNorms() {
data := []float64{3, 4}
v := mat.NewVecDense(2, data)
// L2 norm (Euclidean)
l2 := floats.Norm(data, 2)
fmt.Printf("L2 norm: %.2f\n", l2) // sqrt(3² + 4²) = 5
// L1 norm (Manhattan)
l1 := floats.Norm(data, 1)
fmt.Printf("L1 norm: %.2f\n", l1) // |3| + |4| = 7
// Using mat.Norm
l2Alt := mat.Norm(v, 2)
fmt.Printf("L2 norm (mat): %.2f\n", l2Alt)
}
Output:
L2 norm: 5.00
L1 norm: 7.00
L2 norm (mat): 5.00
Normalizing Vectors
Create a unit vector (length = 1):
func normalizeVector() {
data := []float64{3, 4}
v := mat.NewVecDense(2, data)
// Compute norm
norm := mat.Norm(v, 2)
// Normalize
normalized := mat.NewVecDense(2, nil)
normalized.ScaleVec(1/norm, v)
fmt.Printf("Original: %v\n", mat.Formatted(v.T()))
fmt.Printf("Normalized: %v\n", mat.Formatted(normalized.T()))
fmt.Printf("Norm of normalized: %.6f\n", mat.Norm(normalized, 2))
}
Output:
Original: [3 4]
Normalized: [0.6 0.8]
Norm of normalized: 1.000000
Angle Between Vectors
The angle θ between vectors can be computed using the dot product:
func angleBetweenVectors() {
v1 := mat.NewVecDense(2, []float64{1, 0})
v2 := mat.NewVecDense(2, []float64{1, 1})
// cos(θ) = (v1 · v2) / (||v1|| * ||v2||)
dot := mat.Dot(v1, v2)
norm1 := mat.Norm(v1, 2)
norm2 := mat.Norm(v2, 2)
cosTheta := dot / (norm1 * norm2)
theta := math.Acos(cosTheta)
thetaDegrees := theta * 180 / math.Pi
fmt.Printf("Angle: %.2f radians (%.2f degrees)\n", theta, thetaDegrees)
}
Output:
Angle: 0.79 radians (45.00 degrees)
Working with Raw Slices
Sometimes it’s more efficient to work with raw slices using the floats package:
import "gonum.org/v1/gonum/floats"
func sliceOperations() {
a := []float64{1, 2, 3, 4}
b := []float64{5, 6, 7, 8}
// Element-wise operations modify in place
result := make([]float64, len(a))
copy(result, a)
floats.Add(result, b)
fmt.Printf("a + b = %v\n", result)
// Dot product
dot := floats.Dot(a, b)
fmt.Printf("a · b = %.2f\n", dot)
// Sum
sum := floats.Sum(a)
fmt.Printf("sum(a) = %.2f\n", sum)
// Max
max := floats.Max(a)
fmt.Printf("max(a) = %.2f\n", max)
}
Visualizing Vector Operations
One of Go’s strengths is the gonum/plot library for creating publication-quality visualizations. Here’s how to visualize vector addition:
package main
import (
"image/color"
"math"
"gonum.org/v1/plot"
"gonum.org/v1/plot/plotter"
"gonum.org/v1/plot/vg"
)
func main() {
p := plot.New()
p.Title.Text = "Vector Addition"
p.X.Label.Text = "X"
p.Y.Label.Text = "Y"
p.X.Min, p.X.Max = -1, 8
p.Y.Min, p.Y.Max = -1, 8
// Vectors: v1 = [3,2], v2 = [1,4], sum = [4,6]
drawArrow(p, 0, 0, 3, 2, color.RGBA{R: 66, G: 133, B: 244, A: 255}) // v1 blue
drawArrow(p, 0, 0, 1, 4, color.RGBA{R: 234, G: 67, B: 53, A: 255}) // v2 red
drawArrow(p, 0, 0, 4, 6, color.RGBA{R: 52, G: 168, B: 83, A: 255}) // sum green
p.Save(6*vg.Inch, 6*vg.Inch, "vectors.png")
}
func drawArrow(p *plot.Plot, x1, y1, x2, y2 float64, c color.Color) {
// Line
pts := plotter.XYs{{X: x1, Y: y1}, {X: x2, Y: y2}}
line, _ := plotter.NewLine(pts)
line.Color = c
line.Width = vg.Points(2)
p.Add(line)
// Arrowhead
angle := math.Atan2(y2-y1, x2-x1)
arrowLen := 0.3
for _, da := range []float64{math.Pi / 6, -math.Pi / 6} {
ax := x2 - arrowLen*math.Cos(angle-da)
ay := y2 - arrowLen*math.Sin(angle-da)
arrow, _ := plotter.NewLine(plotter.XYs{{X: x2, Y: y2}, {X: ax, Y: ay}})
arrow.Color = c
arrow.Width = vg.Points(2)
p.Add(arrow)
}
}
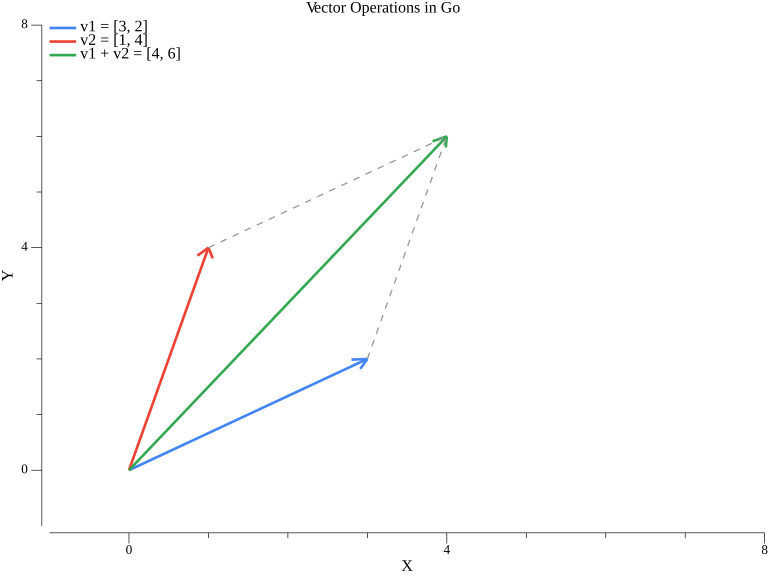
The blue vector v1=[3,2], red vector v2=[1,4], and their sum in green [4,6] form a parallelogram - a fundamental property of vector addition.
Practical Example: Cosine Similarity
Cosine similarity is commonly used in NLP and recommendation systems:
func cosineSimilarity(v1, v2 *mat.VecDense) float64 {
dot := mat.Dot(v1, v2)
norm1 := mat.Norm(v1, 2)
norm2 := mat.Norm(v2, 2)
if norm1 == 0 || norm2 == 0 {
return 0
}
return dot / (norm1 * norm2)
}
func cosineSimilarityExample() {
// Word embeddings (simplified)
king := mat.NewVecDense(4, []float64{0.5, 0.3, 0.8, 0.1})
queen := mat.NewVecDense(4, []float64{0.5, 0.3, 0.7, 0.2})
apple := mat.NewVecDense(4, []float64{0.9, 0.1, 0.1, 0.9})
fmt.Printf("Similarity(king, queen) = %.4f\n",
cosineSimilarity(king, queen))
fmt.Printf("Similarity(king, apple) = %.4f\n",
cosineSimilarity(king, apple))
}
Output:
Similarity(king, queen) = 0.9824
Similarity(king, apple) = 0.5735
Complete Working Example
Here’s a complete program demonstrating all vector operations:
package main
import (
"fmt"
"math"
"gonum.org/v1/gonum/floats"
"gonum.org/v1/gonum/mat"
)
func main() {
// Create vectors
v1 := mat.NewVecDense(3, []float64{1, 2, 3})
v2 := mat.NewVecDense(3, []float64{4, 5, 6})
fmt.Println("=== Vector Operations in Go ===")
fmt.Printf("v1 = %v\n", rawData(v1))
fmt.Printf("v2 = %v\n", rawData(v2))
// Addition
sum := mat.NewVecDense(3, nil)
sum.AddVec(v1, v2)
fmt.Printf("v1 + v2 = %v\n", rawData(sum))
// Dot product
dot := mat.Dot(v1, v2)
fmt.Printf("v1 · v2 = %.2f\n", dot)
// Norms
fmt.Printf("||v1|| = %.4f\n", mat.Norm(v1, 2))
// Normalize
norm := mat.Norm(v1, 2)
unit := mat.NewVecDense(3, nil)
unit.ScaleVec(1/norm, v1)
fmt.Printf("unit(v1) = %v\n", rawData(unit))
fmt.Printf("||unit(v1)|| = %.6f\n", mat.Norm(unit, 2))
}
func rawData(v *mat.VecDense) []float64 {
data := make([]float64, v.Len())
for i := 0; i < v.Len(); i++ {
data[i] = v.AtVec(i)
}
return data
}
Summary
This article covered:
- Setting up gonum for linear algebra in Go
- Creating vectors with
mat.VecDense - Vector operations: addition, subtraction, scalar multiplication
- Dot product using
mat.Dot - Vector norms (L1, L2)
- Normalizing vectors to unit length
- Angle computation between vectors
- Practical application: Cosine similarity
Resources
Linear Algebra: Golang Series - View all articles in this series.
This blog post, titled: "Linear Algebra in Go: Vectors and Basic Operations: Linear Algebra in Go Part 1" by Craig Johnston, is licensed under a Creative Commons Attribution 4.0 International License.
