Linear Algebra in Go: Solving Linear Systems

This article covers solving linear systems in Go using the gonum library, including direct methods with mat.Solve, LU decomposition, and Cholesky decomposition for positive-definite matrices.

Linear Algebra: Golang Series - View all articles in this series.

Previous articles in this series:

1. Linear Algebra in Go: Vectors and Basic Operations
2. Linear Algebra in Go: Matrix Fundamentals

This continues from Part 2: Matrix Fundamentals.

The Linear System Problem

The goal is to solve $\boldsymbol{A}\vec{x} = \vec{b}$ for $\vec{x}$, where $\boldsymbol{A}$ is an $n \times n$ matrix.

Using mat.Solve

The simplest approach in gonum:

package main

import (
    "fmt"
    "gonum.org/v1/gonum/mat"
)

func main() {
    // System: 2x + 3y = 8
    //         x - y = 1
    A := mat.NewDense(2, 2, []float64{
        2, 3,
        1, -1,
    })
    b := mat.NewVecDense(2, []float64{8, 1})

    // Solve Ax = b
    var x mat.VecDense
    err := x.SolveVec(A, b)
    if err != nil {
        fmt.Printf("Error: %v\n", err)
        return
    }

    fmt.Println("Solution:")
    fmt.Printf("x = %.4f\n", x.AtVec(0))
    fmt.Printf("y = %.4f\n", x.AtVec(1))

    // Verify: A*x should equal b
    var result mat.VecDense
    result.MulVec(A, &x)
    fmt.Printf("\nVerification (A*x): [%.2f, %.2f]\n",
        result.AtVec(0), result.AtVec(1))
}

Output:

Solution:
x = 2.2000
y = 1.2000

Verification (A*x): [8.00, 1.00]

Visualizing the Solution

A system of two linear equations represents two lines. The solution is their intersection:

package main

import (
    "image/color"

    "gonum.org/v1/plot"
    "gonum.org/v1/plot/plotter"
    "gonum.org/v1/plot/vg"
    "gonum.org/v1/plot/vg/draw"
)

func main() {
    p := plot.New()
    p.Title.Text = "Linear System: Two Lines Intersecting"
    p.X.Label.Text = "x"
    p.Y.Label.Text = "y"
    p.X.Min, p.X.Max = -1, 5
    p.Y.Min, p.Y.Max = -1, 4

    // Line 1: 2x + 3y = 8  =>  y = (8 - 2x) / 3
    line1Pts := make(plotter.XYs, 100)
    for i := range line1Pts {
        x := -1.0 + float64(i)*0.06
        line1Pts[i] = plotter.XY{X: x, Y: (8 - 2*x) / 3}
    }
    l1, _ := plotter.NewLine(line1Pts)
    l1.Color = color.RGBA{R: 66, G: 133, B: 244, A: 255}
    l1.Width = vg.Points(2)

    // Line 2: x - y = 1  =>  y = x - 1
    line2Pts := make(plotter.XYs, 100)
    for i := range line2Pts {
        x := -1.0 + float64(i)*0.06
        line2Pts[i] = plotter.XY{X: x, Y: x - 1}
    }
    l2, _ := plotter.NewLine(line2Pts)
    l2.Color = color.RGBA{R: 234, G: 67, B: 53, A: 255}
    l2.Width = vg.Points(2)

    // Solution point (2.2, 1.2)
    solPts := plotter.XYs{{X: 2.2, Y: 1.2}}
    sol, _ := plotter.NewScatter(solPts)
    sol.GlyphStyle.Color = color.RGBA{R: 52, G: 168, B: 83, A: 255}
    sol.GlyphStyle.Radius = vg.Points(6)
    sol.GlyphStyle.Shape = draw.CircleGlyph{}

    p.Add(l1, l2, sol)
    p.Save(6*vg.Inch, 5*vg.Inch, "systems.png")
}

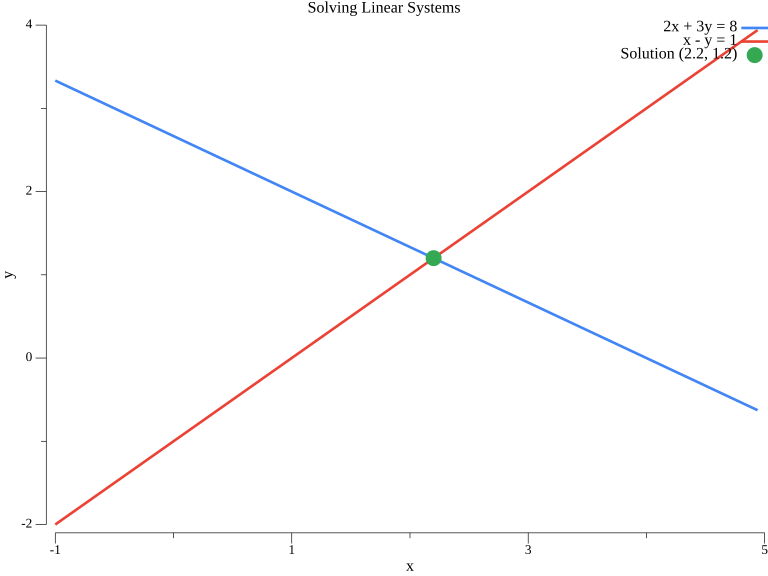
The blue line represents 2x + 3y = 8, the red line represents x - y = 1, and the green point marks the solution (2.2, 1.2).

LU Decomposition

LU decomposition factors a matrix as $\boldsymbol{A} = \boldsymbol{L}\boldsymbol{U}$ where $\boldsymbol{L}$ is lower triangular and $\boldsymbol{U}$ is upper triangular:

import "gonum.org/v1/gonum/mat"

func luDecomposition() {
    A := mat.NewDense(3, 3, []float64{
        2, -1, 0,
        -1, 2, -1,
        0, -1, 2,
    })

    // Compute LU decomposition
    var lu mat.LU
    lu.Factorize(A)

    // Extract L and U
    var L, U mat.TriDense
    lu.LTo(&L)
    lu.UTo(&U)

    fmt.Println("L (lower triangular):")
    fmt.Printf("%v\n", mat.Formatted(&L))

    fmt.Println("\nU (upper triangular):")
    fmt.Printf("%v\n", mat.Formatted(&U))

    // Solve using LU
    b := mat.NewVecDense(3, []float64{1, 0, 1})
    var x mat.VecDense
    err := lu.SolveVecTo(&x, false, b)
    if err != nil {
        fmt.Printf("Error: %v\n", err)
        return
    }

    fmt.Println("\nSolution x:")
    fmt.Printf("%v\n", mat.Formatted(&x))
}

Cholesky Decomposition

For symmetric positive-definite matrices, Cholesky decomposition is more efficient: $\boldsymbol{A} = \boldsymbol{L}\boldsymbol{L}^T$

func choleskyDecomposition() {
    // Symmetric positive-definite matrix
    A := mat.NewSymDense(3, []float64{
        4, 2, 2,
        2, 5, 1,
        2, 1, 6,
    })

    // Compute Cholesky decomposition
    var chol mat.Cholesky
    ok := chol.Factorize(A)
    if !ok {
        fmt.Println("Matrix is not positive-definite")
        return
    }

    // Extract L
    var L mat.TriDense
    chol.LTo(&L)

    fmt.Println("Cholesky factor L:")
    fmt.Printf("%v\n", mat.Formatted(&L))

    // Solve using Cholesky
    b := mat.NewVecDense(3, []float64{1, 2, 3})
    var x mat.VecDense
    err := chol.SolveVecTo(&x, b)
    if err != nil {
        fmt.Printf("Error: %v\n", err)
        return
    }

    fmt.Println("\nSolution:")
    fmt.Printf("%v\n", mat.Formatted(&x))
}

QR Decomposition for Least Squares

For overdetermined systems (more equations than unknowns), use QR decomposition:

func qrLeastSquares() {
    // Overdetermined system: 4 equations, 2 unknowns
    A := mat.NewDense(4, 2, []float64{
        1, 1,
        1, 2,
        1, 3,
        1, 4,
    })
    b := mat.NewVecDense(4, []float64{2.1, 3.9, 6.2, 7.8})

    // QR decomposition
    var qr mat.QR
    qr.Factorize(A)

    // Solve least squares
    var x mat.VecDense
    err := qr.SolveVecTo(&x, false, b)
    if err != nil {
        fmt.Printf("Error: %v\n", err)
        return
    }

    fmt.Println("Least squares solution:")
    fmt.Printf("Intercept: %.4f\n", x.AtVec(0))
    fmt.Printf("Slope: %.4f\n", x.AtVec(1))

    // Compute residuals
    var residuals mat.VecDense
    residuals.MulVec(A, &x)
    residuals.SubVec(&residuals, b)

    residualNorm := mat.Norm(&residuals, 2)
    fmt.Printf("\nResidual norm: %.4f\n", residualNorm)
}

Benchmarking: Go vs Python

Go typically offers significant performance advantages:

import (
    "fmt"
    "time"
    "gonum.org/v1/gonum/mat"
)

func benchmarkSolve() {
    sizes := []int{100, 500, 1000}

    for _, n := range sizes {
        // Generate random matrix and vector
        data := make([]float64, n*n)
        for i := range data {
            data[i] = float64(i%17) - 8
        }
        A := mat.NewDense(n, n, data)

        bData := make([]float64, n)
        for i := range bData {
            bData[i] = float64(i % 11)
        }
        b := mat.NewVecDense(n, bData)

        // Time the solve
        start := time.Now()
        var x mat.VecDense
        x.SolveVec(A, b)
        elapsed := time.Since(start)

        fmt.Printf("Size %4d x %4d: %v\n", n, n, elapsed)
    }
}

Condition Number

Check numerical stability by computing the condition number:

func conditionNumber() {
    A := mat.NewDense(3, 3, []float64{
        1, 2, 3,
        4, 5, 6,
        7, 8, 9.0001,  // Nearly singular
    })

    // SVD to compute condition number
    var svd mat.SVD
    svd.Factorize(A, mat.SVDThin)

    values := svd.Values(nil)
    cond := values[0] / values[len(values)-1]

    fmt.Printf("Singular values: %v\n", values)
    fmt.Printf("Condition number: %.2e\n", cond)
}

Summary

This article covered:

• Direct solving with mat.Solve
• LU decomposition for general square matrices
• Cholesky decomposition for symmetric positive-definite matrices
• QR decomposition for least squares
• Performance benchmarking
• Condition number for numerical stability

The next article covers eigenvalue problems in Go.

Resources

• Gonum mat Package
• Linear Systems in Python

Next: Eigenvalue Problems

Check out the next article in this series, Linear Algebra in Go: Eigenvalue Problems.

Linear Algebra: Golang Series - View all articles in this series.

This blog post, titled: "Linear Algebra in Go: Solving Linear Systems: Linear Algebra in Go Part 3" by Craig Johnston, is licensed under a Creative Commons Attribution 4.0 International License.