This article covers Singular Value Decomposition (SVD) and related matrix decompositions in Go. SVD is fundamental to many applications including dimensionality reduction, pseudoinverse computation, and low-rank approximation.
Linear Algebra: Golang Series - View all articles in this series.
Previous articles in this series:
- Linear Algebra in Go: Vectors and Basic Operations
- Linear Algebra in Go: Matrix Fundamentals
- Linear Algebra in Go: Solving Linear Systems
- Linear Algebra in Go: Eigenvalue Problems
This continues from Part 4: Eigenvalue Problems.
SVD Decomposition
The SVD factors a matrix as $\boldsymbol{A} = \boldsymbol{U}\boldsymbol{\Sigma}\boldsymbol{V}^T$:
package main
import (
"fmt"
"gonum.org/v1/gonum/mat"
)
func main() {
A := mat.NewDense(4, 3, []float64{
1, 2, 3,
4, 5, 6,
7, 8, 9,
10, 11, 12,
})
var svd mat.SVD
ok := svd.Factorize(A, mat.SVDThin)
if !ok {
fmt.Println("SVD factorization failed")
return
}
// Get singular values
values := svd.Values(nil)
fmt.Println("Singular values:")
for i, v := range values {
fmt.Printf(" σ%d = %.6f\n", i+1, v)
}
// Get U and V matrices
var U, V mat.Dense
svd.UTo(&U)
svd.VTo(&V)
fmt.Println("\nU matrix:")
fmt.Printf("%v\n", mat.Formatted(&U, mat.Prefix(" ")))
fmt.Println("\nV matrix:")
fmt.Printf("%v\n", mat.Formatted(&V, mat.Prefix(" ")))
}
Visualizing Singular Value Decay
Singular values typically decay rapidly, which enables low-rank approximations:
package main
import (
"fmt"
"math"
"gonum.org/v1/plot"
"gonum.org/v1/plot/plotter"
"gonum.org/v1/plot/vg"
"image/color"
)
func main() {
p := plot.New()
p.Title.Text = "Singular Value Decay"
p.Y.Label.Text = "Singular Value"
p.X.Label.Text = "Index"
// Simulate typical singular value decay
n := 15
vals := make(plotter.Values, n)
for i := 0; i < n; i++ {
vals[i] = 50 * math.Exp(-0.3*float64(i))
}
bars, _ := plotter.NewBarChart(vals, vg.Points(20))
bars.Color = color.RGBA{R: 66, G: 133, B: 244, A: 255}
p.Add(bars)
labels := make([]string, n)
for i := 0; i < n; i++ {
labels[i] = fmt.Sprintf("%d", i+1)
}
p.NominalX(labels...)
p.Save(6*vg.Inch, 4*vg.Inch, "svd.png")
}
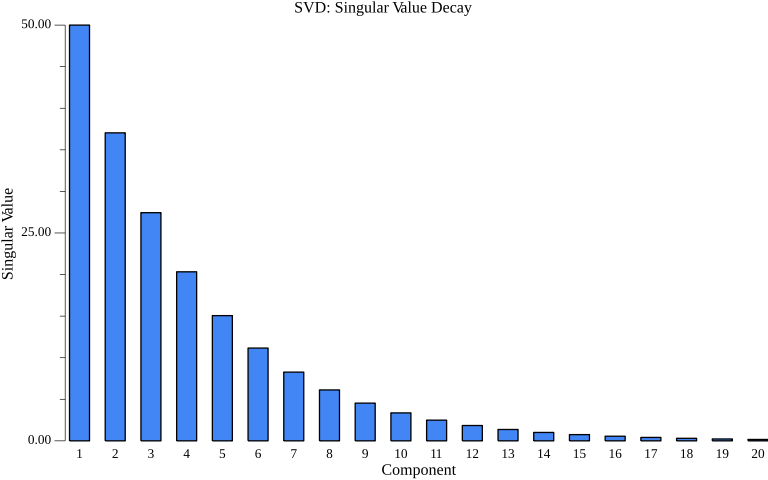
The rapid decay of singular values explains why low-rank approximations work well - most of the “information” is captured in the first few components.
Low-Rank Approximation
Keep only the top k singular values:
func lowRankApprox(A *mat.Dense, k int) *mat.Dense {
var svd mat.SVD
svd.Factorize(A, mat.SVDThin)
values := svd.Values(nil)
var U, V mat.Dense
svd.UTo(&U)
svd.VTo(&V)
rows, cols := A.Dims()
// Truncate to k components
Uk := U.Slice(0, rows, 0, k).(*mat.Dense)
Vk := V.Slice(0, cols, 0, k).(*mat.Dense)
// Construct diagonal matrix with top k singular values
Sk := mat.NewDiagDense(k, values[:k])
// Compute U_k * S_k * V_k^T
var temp mat.Dense
temp.Mul(Uk, Sk)
var result mat.Dense
result.Mul(&temp, Vk.T())
return &result
}
func lowRankExample() {
A := mat.NewDense(5, 4, []float64{
1, 2, 3, 4,
5, 6, 7, 8,
9, 10, 11, 12,
13, 14, 15, 16,
17, 18, 19, 20,
})
fmt.Println("Original matrix:")
fmt.Printf("%v\n\n", mat.Formatted(A))
for k := 1; k <= 3; k++ {
Ak := lowRankApprox(A, k)
diff := mat.NewDense(5, 4, nil)
diff.Sub(A, Ak)
error := mat.Norm(diff, 2)
fmt.Printf("Rank-%d approximation error: %.6f\n", k, error)
}
}
Pseudoinverse via SVD
Compute the Moore-Penrose pseudoinverse:
func pseudoinverse(A *mat.Dense) *mat.Dense {
var svd mat.SVD
svd.Factorize(A, mat.SVDThin)
values := svd.Values(nil)
var U, V mat.Dense
svd.UTo(&U)
svd.VTo(&V)
rows, cols := A.Dims()
minDim := min(rows, cols)
// Invert non-zero singular values
tol := 1e-10 * values[0]
sInv := make([]float64, minDim)
for i, s := range values {
if s > tol {
sInv[i] = 1.0 / s
}
}
// A+ = V * S+ * U^T
SInv := mat.NewDiagDense(minDim, sInv)
var temp mat.Dense
temp.Mul(&V, SInv)
var pinv mat.Dense
pinv.Mul(&temp, U.T())
return &pinv
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
QR Decomposition
Factor $\boldsymbol{A} = \boldsymbol{Q}\boldsymbol{R}$:
func qrDecomposition() {
A := mat.NewDense(4, 3, []float64{
1, 2, 3,
4, 5, 6,
7, 8, 10,
10, 11, 13,
})
var qr mat.QR
qr.Factorize(A)
var Q, R mat.Dense
qr.QTo(&Q)
qr.RTo(&R)
fmt.Println("Q (orthogonal):")
fmt.Printf("%v\n\n", mat.Formatted(&Q, mat.Prefix(" ")))
fmt.Println("R (upper triangular):")
fmt.Printf("%v\n\n", mat.Formatted(&R, mat.Prefix(" ")))
// Verify Q is orthogonal: Q^T * Q = I
var QTQ mat.Dense
QTQ.Mul(Q.T(), &Q)
fmt.Println("Q^T * Q (should be identity):")
fmt.Printf("%v\n", mat.Formatted(&QTQ, mat.Prefix(" ")))
}
Condition Number
Compute condition number using SVD:
func conditionNumber(A *mat.Dense) float64 {
var svd mat.SVD
svd.Factorize(A, mat.SVDNone)
values := svd.Values(nil)
return values[0] / values[len(values)-1]
}
func conditionExample() {
// Well-conditioned
A := mat.NewDense(3, 3, []float64{
1, 0, 0,
0, 2, 0,
0, 0, 3,
})
// Ill-conditioned
B := mat.NewDense(3, 3, []float64{
1, 1, 1,
1, 1, 1.0001,
1, 1.0001, 1,
})
fmt.Printf("Well-conditioned matrix: κ = %.2f\n", conditionNumber(A))
fmt.Printf("Ill-conditioned matrix: κ = %.2e\n", conditionNumber(B))
}
Summary
This article covered:
- SVD decomposition: $\boldsymbol{A} = \boldsymbol{U}\boldsymbol{\Sigma}\boldsymbol{V}^T$
- Low-rank approximation using truncated SVD
- Pseudoinverse computation
- QR decomposition
- Condition number for numerical stability
Resources
Linear Algebra: Golang Series - View all articles in this series.
Note: This blog is a collection of personal notes. Making them public encourages me to think beyond the limited scope of the current problem I'm trying to solve or concept I'm implementing, and hopefully provides something useful to my team and others.
This blog post, titled: "Linear Algebra in Go: SVD and Decompositions: Linear Algebra in Go Part 5" by Craig Johnston, is licensed under a Creative Commons Attribution 4.0 International License.
