Linear Algebra in Go: Building a Regression Library

This article demonstrates building a regression library in Go from scratch using gonum: ordinary least squares, ridge regression, and cross-validation.

Linear Algebra: Golang Series - View all articles in this series.

Previous articles in this series:

This continues from Part 6: Statistics and Data Analysis.

Linear Regression Structure

package regression

import (
    "gonum.org/v1/gonum/mat"
)

// LinearRegression implements OLS regression
type LinearRegression struct {
    Weights     *mat.VecDense
    Intercept   float64
    FitIntercept bool
}

// NewLinearRegression creates a new regression model
func NewLinearRegression(fitIntercept bool) *LinearRegression {
    return &LinearRegression{
        FitIntercept: fitIntercept,
    }
}

Fit Method

// Fit trains the model using ordinary least squares
func (lr *LinearRegression) Fit(X *mat.Dense, y *mat.VecDense) error {
    rows, cols := X.Dims()

    // Add intercept column if needed
    var Xb *mat.Dense
    if lr.FitIntercept {
        Xb = mat.NewDense(rows, cols+1, nil)
        for i := 0; i < rows; i++ {
            Xb.Set(i, 0, 1.0)  // Intercept column
            for j := 0; j < cols; j++ {
                Xb.Set(i, j+1, X.At(i, j))
            }
        }
    } else {
        Xb = X
    }

    // Solve normal equations: (X^T X) w = X^T y
    _, nCols := Xb.Dims()
    var XtX mat.Dense
    XtX.Mul(Xb.T(), Xb)

    var Xty mat.VecDense
    Xty.MulVec(Xb.T(), y)

    // Solve for weights
    lr.Weights = mat.NewVecDense(nCols, nil)
    err := lr.Weights.SolveVec(&XtX, &Xty)
    if err != nil {
        return err
    }

    // Extract intercept if fitted
    if lr.FitIntercept {
        lr.Intercept = lr.Weights.AtVec(0)
        // Remove intercept from weights
        newWeights := mat.NewVecDense(nCols-1, nil)
        for i := 1; i < nCols; i++ {
            newWeights.SetVec(i-1, lr.Weights.AtVec(i))
        }
        lr.Weights = newWeights
    }

    return nil
}

Predict Method

// Predict generates predictions for new data
func (lr *LinearRegression) Predict(X *mat.Dense) *mat.VecDense {
    rows, _ := X.Dims()

    predictions := mat.NewVecDense(rows, nil)
    predictions.MulVec(X, lr.Weights)

    // Add intercept
    if lr.FitIntercept {
        for i := 0; i < rows; i++ {
            predictions.SetVec(i, predictions.AtVec(i)+lr.Intercept)
        }
    }

    return predictions
}

Visualizing Regression

Here’s a visualization of a linear regression fit:

package main

import (
    "fmt"
    "image/color"
    "math/rand"

    "gonum.org/v1/gonum/stat"
    "gonum.org/v1/plot"
    "gonum.org/v1/plot/plotter"
    "gonum.org/v1/plot/vg"
)

func main() {
    rand.Seed(42)
    p := plot.New()
    p.Title.Text = "Linear Regression with Gonum"
    p.X.Label.Text = "X"
    p.Y.Label.Text = "Y"

    n := 40
    pts := make(plotter.XYs, n)
    xData := make([]float64, n)
    yData := make([]float64, n)

    for i := 0; i < n; i++ {
        x := float64(i) / 4.0
        y := 2 + 1.5*x + rand.NormFloat64()*1.5
        pts[i] = plotter.XY{X: x, Y: y}
        xData[i] = x
        yData[i] = y
    }

    scatter, _ := plotter.NewScatter(pts)
    scatter.GlyphStyle.Color = color.RGBA{R: 66, G: 133, B: 244, A: 200}
    scatter.GlyphStyle.Radius = vg.Points(5)

    alpha, beta := stat.LinearRegression(xData, yData, nil, false)
    linePts := plotter.XYs{{X: 0, Y: alpha}, {X: 10, Y: alpha + 10*beta}}
    line, _ := plotter.NewLine(linePts)
    line.Color = color.RGBA{R: 234, G: 67, B: 53, A: 255}
    line.Width = vg.Points(2)

    p.Add(scatter, line)
    p.Legend.Add("Data", scatter)
    p.Legend.Add(fmt.Sprintf("y = %.1f + %.1fx", alpha, beta), line)
    p.Legend.Top = true

    p.Save(6*vg.Inch, 5*vg.Inch, "regression.png")
}

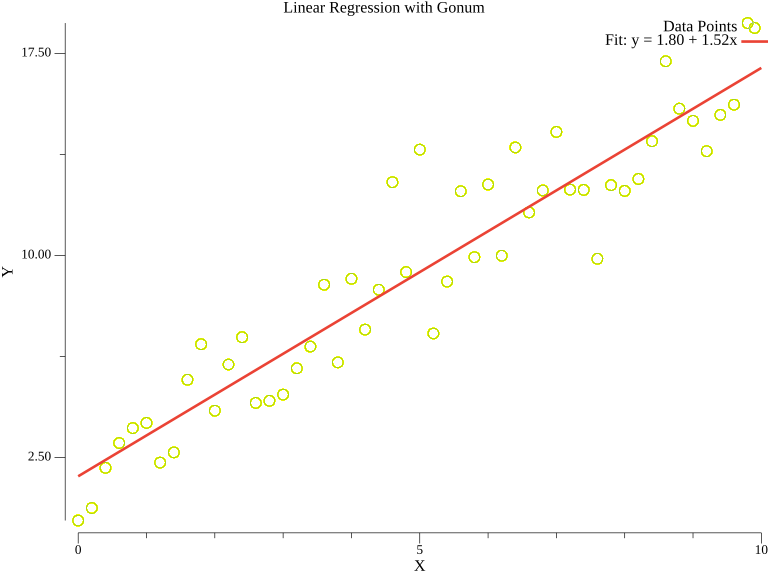
Linear regression showing data points and fitted line

The blue points represent observed data, and the red line shows the fitted regression model. The legend displays the learned equation.

Ridge Regression

// RidgeRegression implements L2-regularized regression
type RidgeRegression struct {
    Weights      *mat.VecDense
    Intercept    float64
    Alpha        float64
    FitIntercept bool
}

func NewRidgeRegression(alpha float64, fitIntercept bool) *RidgeRegression {
    return &RidgeRegression{
        Alpha:        alpha,
        FitIntercept: fitIntercept,
    }
}

func (rr *RidgeRegression) Fit(X *mat.Dense, y *mat.VecDense) error {
    rows, cols := X.Dims()

    // Add intercept column
    var Xb *mat.Dense
    if rr.FitIntercept {
        Xb = mat.NewDense(rows, cols+1, nil)
        for i := 0; i < rows; i++ {
            Xb.Set(i, 0, 1.0)
            for j := 0; j < cols; j++ {
                Xb.Set(i, j+1, X.At(i, j))
            }
        }
    } else {
        Xb = X
    }

    _, nCols := Xb.Dims()

    // (X^T X + alpha * I) w = X^T y
    var XtX mat.Dense
    XtX.Mul(Xb.T(), Xb)

    // Add regularization term (skip intercept)
    for i := 0; i < nCols; i++ {
        if rr.FitIntercept && i == 0 {
            continue  // Don't regularize intercept
        }
        XtX.Set(i, i, XtX.At(i, i)+rr.Alpha)
    }

    var Xty mat.VecDense
    Xty.MulVec(Xb.T(), y)

    rr.Weights = mat.NewVecDense(nCols, nil)
    err := rr.Weights.SolveVec(&XtX, &Xty)
    if err != nil {
        return err
    }

    if rr.FitIntercept {
        rr.Intercept = rr.Weights.AtVec(0)
        newWeights := mat.NewVecDense(nCols-1, nil)
        for i := 1; i < nCols; i++ {
            newWeights.SetVec(i-1, rr.Weights.AtVec(i))
        }
        rr.Weights = newWeights
    }

    return nil
}

Cross-Validation

// CrossValidate performs k-fold cross-validation
func CrossValidate(X *mat.Dense, y *mat.VecDense, k int) []float64 {
    rows, _ := X.Dims()
    foldSize := rows / k
    scores := make([]float64, k)

    for fold := 0; fold < k; fold++ {
        // Split data
        testStart := fold * foldSize
        testEnd := testStart + foldSize

        // Create train/test splits
        XTrain, yTrain, XTest, yTest := splitData(X, y, testStart, testEnd)

        // Train model
        model := NewLinearRegression(true)
        model.Fit(XTrain, yTrain)

        // Evaluate
        predictions := model.Predict(XTest)
        scores[fold] = rSquared(yTest, predictions)
    }

    return scores
}

func rSquared(yTrue, yPred *mat.VecDense) float64 {
    n := yTrue.Len()

    // Mean of y
    var sum float64
    for i := 0; i < n; i++ {
        sum += yTrue.AtVec(i)
    }
    mean := sum / float64(n)

    // SS_res and SS_tot
    var ssRes, ssTot float64
    for i := 0; i < n; i++ {
        diff := yTrue.AtVec(i) - yPred.AtVec(i)
        ssRes += diff * diff
        diff = yTrue.AtVec(i) - mean
        ssTot += diff * diff
    }

    return 1 - ssRes/ssTot
}

Usage Example

func main() {
    // Generate sample data
    X := mat.NewDense(100, 3, nil)
    y := mat.NewVecDense(100, nil)

    for i := 0; i < 100; i++ {
        x1 := rand.Float64() * 10
        x2 := rand.Float64() * 10
        x3 := rand.Float64() * 10
        X.Set(i, 0, x1)
        X.Set(i, 1, x2)
        X.Set(i, 2, x3)
        y.SetVec(i, 2 + 3*x1 - 1.5*x2 + 0.5*x3 + rand.NormFloat64())
    }

    // Fit OLS
    ols := NewLinearRegression(true)
    ols.Fit(X, y)
    fmt.Printf("OLS Weights: %v\n", ols.Weights)
    fmt.Printf("OLS Intercept: %.4f\n", ols.Intercept)

    // Fit Ridge
    ridge := NewRidgeRegression(1.0, true)
    ridge.Fit(X, y)
    fmt.Printf("Ridge Weights: %v\n", ridge.Weights)

    // Cross-validation
    scores := CrossValidate(X, y, 5)
    fmt.Printf("CV R² scores: %v\n", scores)
}

Summary

This article built:

LinearRegression using normal equations
RidgeRegression with L2 regularization
Cross-validation for model evaluation
R-squared metric computation

Resources

Linear Algebra: Golang Series - View all articles in this series.

Note: This blog is a collection of personal notes. Making them public encourages me to think beyond the limited scope of the current problem I'm trying to solve or concept I'm implementing, and hopefully provides something useful to my team and others.

This blog post, titled: "Linear Algebra in Go: Building a Regression Library: Linear Algebra in Go Part 7" by Craig Johnston, is licensed under a Creative Commons Attribution 4.0 International License.