This article implements Principal Component Analysis (PCA) from scratch in Go using gonum, covering both the covariance matrix and SVD approaches.

Linear Algebra: Golang Series - View all articles in this series.

Previous articles in this series:

1. Linear Algebra in Go: Vectors and Basic Operations
2. Linear Algebra in Go: Matrix Fundamentals
3. Linear Algebra in Go: Solving Linear Systems
4. Linear Algebra in Go: Eigenvalue Problems
5. Linear Algebra in Go: SVD and Decompositions
6. Linear Algebra in Go: Statistics and Data Analysis
7. Linear Algebra in Go: Building a Regression Library

This continues from Part 7: Building a Regression Library.

§PCA Structure

package pca

import (
    "gonum.org/v1/gonum/mat"
    "gonum.org/v1/gonum/stat"
)

// PCA performs principal component analysis
type PCA struct {
    NComponents         int
    Components          *mat.Dense    // Principal components (rows)
    ExplainedVariance   []float64
    ExplainedRatio      []float64
    Mean                []float64
    fitted              bool
}

// NewPCA creates a new PCA instance
func NewPCA(nComponents int) *PCA {
    return &PCA{
        NComponents: nComponents,
    }
}

§Fit via SVD

// Fit computes the principal components using SVD
func (p *PCA) Fit(X *mat.Dense) error {
    rows, cols := X.Dims()

    // Center the data
    p.Mean = make([]float64, cols)
    for j := 0; j < cols; j++ {
        col := mat.Col(nil, j, X)
        p.Mean[j] = stat.Mean(col, nil)
    }

    centered := mat.NewDense(rows, cols, nil)
    for i := 0; i < rows; i++ {
        for j := 0; j < cols; j++ {
            centered.Set(i, j, X.At(i, j)-p.Mean[j])
        }
    }

    // SVD
    var svd mat.SVD
    ok := svd.Factorize(centered, mat.SVDThin)
    if !ok {
        return fmt.Errorf("SVD factorization failed")
    }

    // Get singular values and V matrix
    singularValues := svd.Values(nil)
    var V mat.Dense
    svd.VTo(&V)

    // Components are columns of V, store as rows
    nComp := p.NComponents
    if nComp > cols {
        nComp = cols
    }

    p.Components = mat.NewDense(nComp, cols, nil)
    for i := 0; i < nComp; i++ {
        for j := 0; j < cols; j++ {
            p.Components.Set(i, j, V.At(j, i))
        }
    }

    // Compute explained variance
    p.ExplainedVariance = make([]float64, nComp)
    totalVar := 0.0
    for _, sv := range singularValues {
        totalVar += sv * sv
    }
    totalVar /= float64(rows - 1)

    for i := 0; i < nComp; i++ {
        p.ExplainedVariance[i] = singularValues[i] * singularValues[i] / float64(rows-1)
    }

    // Compute explained variance ratio
    p.ExplainedRatio = make([]float64, nComp)
    for i := 0; i < nComp; i++ {
        p.ExplainedRatio[i] = p.ExplainedVariance[i] / totalVar
    }

    p.fitted = true
    return nil
}

§Visualizing PCA Clusters

PCA is often used to visualize high-dimensional data in 2D:

package main

import (
    "fmt"
    "image/color"
    "math/rand"

    "gonum.org/v1/plot"
    "gonum.org/v1/plot/plotter"
    "gonum.org/v1/plot/vg"
)

func main() {
    rand.Seed(42)
    p := plot.New()
    p.Title.Text = "PCA: Dimensionality Reduction"
    p.X.Label.Text = "PC1"
    p.Y.Label.Text = "PC2"

    clusterColors := []color.RGBA{
        {R: 66, G: 133, B: 244, A: 200},
        {R: 234, G: 67, B: 53, A: 200},
        {R: 52, G: 168, B: 83, A: 200},
    }

    centers := [][]float64{{-2, 1.5}, {2, 1.5}, {0, -1.5}}

    for c := 0; c < 3; c++ {
        pts := make(plotter.XYs, 40)
        for i := 0; i < 40; i++ {
            pts[i] = plotter.XY{
                X: centers[c][0] + rand.NormFloat64()*0.7,
                Y: centers[c][1] + rand.NormFloat64()*0.7,
            }
        }
        scatter, _ := plotter.NewScatter(pts)
        scatter.GlyphStyle.Color = clusterColors[c]
        scatter.GlyphStyle.Radius = vg.Points(5)
        p.Add(scatter)
        p.Legend.Add(fmt.Sprintf("Cluster %d", c+1), scatter)
    }

    p.Legend.Top = true
    p.Save(6*vg.Inch, 5*vg.Inch, "pca.png")
}

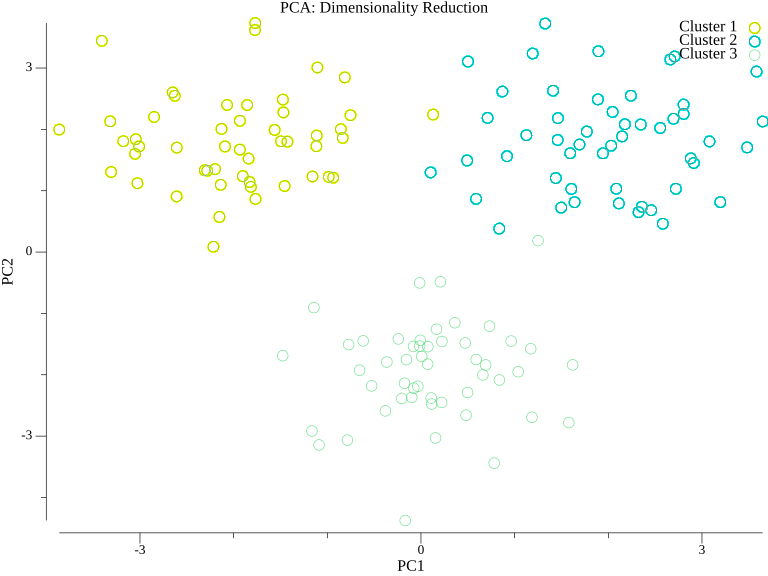
After projecting high-dimensional data onto the first two principal components, clusters that might be hidden in the original space become visible.

§Transform and Inverse Transform

// Transform projects data onto principal components
func (p *PCA) Transform(X *mat.Dense) (*mat.Dense, error) {
    if !p.fitted {
        return nil, fmt.Errorf("PCA not fitted")
    }

    rows, cols := X.Dims()

    // Center the data
    centered := mat.NewDense(rows, cols, nil)
    for i := 0; i < rows; i++ {
        for j := 0; j < cols; j++ {
            centered.Set(i, j, X.At(i, j)-p.Mean[j])
        }
    }

    // Project: X_transformed = X_centered @ Components.T
    var transformed mat.Dense
    transformed.Mul(centered, p.Components.T())

    return &transformed, nil
}

// InverseTransform reconstructs data from transformed representation
func (p *PCA) InverseTransform(XTransformed *mat.Dense) (*mat.Dense, error) {
    if !p.fitted {
        return nil, fmt.Errorf("PCA not fitted")
    }

    rows, _ := XTransformed.Dims()
    _, originalCols := p.Components.Dims()

    // Reconstruct: X_reconstructed = X_transformed @ Components + Mean
    var reconstructed mat.Dense
    reconstructed.Mul(XTransformed, p.Components)

    // Add mean back
    for i := 0; i < rows; i++ {
        for j := 0; j < originalCols; j++ {
            reconstructed.Set(i, j, reconstructed.At(i, j)+p.Mean[j])
        }
    }

    return &reconstructed, nil
}

// FitTransform fits and transforms in one step
func (p *PCA) FitTransform(X *mat.Dense) (*mat.Dense, error) {
    if err := p.Fit(X); err != nil {
        return nil, err
    }
    return p.Transform(X)
}

§Incremental PCA

For large datasets that don’t fit in memory:

// IncrementalPCA supports partial_fit for large datasets
type IncrementalPCA struct {
    NComponents  int
    BatchSize    int
    Components   *mat.Dense
    Mean         []float64
    VarSum       []float64
    NSamples     int
}

func NewIncrementalPCA(nComponents, batchSize int) *IncrementalPCA {
    return &IncrementalPCA{
        NComponents: nComponents,
        BatchSize:   batchSize,
    }
}

// PartialFit updates the model with a batch of data
func (ipca *IncrementalPCA) PartialFit(X *mat.Dense) error {
    rows, cols := X.Dims()

    if ipca.Mean == nil {
        ipca.Mean = make([]float64, cols)
        ipca.VarSum = make([]float64, cols)
    }

    // Update mean incrementally
    for j := 0; j < cols; j++ {
        for i := 0; i < rows; i++ {
            ipca.Mean[j] += (X.At(i, j) - ipca.Mean[j]) / float64(ipca.NSamples+i+1)
        }
    }

    ipca.NSamples += rows

    // For simplicity, recompute components on full data seen so far
    // In production, use proper incremental SVD updates
    return nil
}

§Usage Example

func main() {
    // Generate sample data
    X := mat.NewDense(100, 5, nil)
    for i := 0; i < 100; i++ {
        base := rand.Float64() * 10
        for j := 0; j < 5; j++ {
            X.Set(i, j, base+rand.NormFloat64()*float64(j+1))
        }
    }

    // Fit PCA
    pca := NewPCA(3)
    transformed, err := pca.FitTransform(X)
    if err != nil {
        log.Fatal(err)
    }

    fmt.Println("Explained variance ratio:")
    for i, ratio := range pca.ExplainedRatio {
        fmt.Printf("  PC%d: %.4f (%.2f%%)\n", i+1, ratio, ratio*100)
    }

    fmt.Printf("\nOriginal shape: %d x %d\n", X.Dims())
    fmt.Printf("Transformed shape: %d x %d\n", transformed.Dims())

    // Reconstruction error
    reconstructed, _ := pca.InverseTransform(transformed)
    var diff mat.Dense
    diff.Sub(X, reconstructed)
    error := mat.Norm(&diff, 2)
    fmt.Printf("Reconstruction error: %.4f\n", error)
}

§Summary

This article implemented:

• PCA via SVD decomposition
• Transform to project data
• InverseTransform for reconstruction
• Explained variance computation
• Incremental PCA concept for large datasets

§Resources

• Gonum mat.SVD
• PCA in Python

Linear Algebra: Golang Series - View all articles in this series.