This article implements neural network foundations in Go using gonum: a perceptron, forward propagation, and backpropagation from scratch.
Linear Algebra: Golang Series - View all articles in this series.
Previous articles in this series:
- Linear Algebra in Go: Vectors and Basic Operations
- Linear Algebra in Go: Matrix Fundamentals
- Linear Algebra in Go: Solving Linear Systems
- Linear Algebra in Go: Eigenvalue Problems
- Linear Algebra in Go: SVD and Decompositions
- Linear Algebra in Go: Statistics and Data Analysis
- Linear Algebra in Go: Building a Regression Library
- Linear Algebra in Go: PCA Implementation
This continues from Part 8: PCA Implementation.
Perceptron
The simplest neural network unit:
package nn
import (
"math"
"gonum.org/v1/gonum/mat"
)
// Perceptron implements a single-layer perceptron
type Perceptron struct {
Weights *mat.VecDense
Bias float64
LearningRate float64
}
// NewPerceptron creates a new perceptron
func NewPerceptron(nFeatures int, lr float64) *Perceptron {
weights := mat.NewVecDense(nFeatures, nil)
// Initialize with small random values
for i := 0; i < nFeatures; i++ {
weights.SetVec(i, (rand.Float64()-0.5)*0.1)
}
return &Perceptron{
Weights: weights,
Bias: 0,
LearningRate: lr,
}
}
// Predict returns the perceptron output
func (p *Perceptron) Predict(x *mat.VecDense) int {
sum := mat.Dot(p.Weights, x) + p.Bias
if sum >= 0 {
return 1
}
return 0
}
// Train updates weights based on a single sample
func (p *Perceptron) Train(x *mat.VecDense, target int) {
prediction := p.Predict(x)
error := float64(target - prediction)
// Update weights: w = w + lr * error * x
for i := 0; i < p.Weights.Len(); i++ {
p.Weights.SetVec(i, p.Weights.AtVec(i)+p.LearningRate*error*x.AtVec(i))
}
p.Bias += p.LearningRate * error
}
// Fit trains on a dataset for multiple epochs
func (p *Perceptron) Fit(X *mat.Dense, y []int, epochs int) []float64 {
rows, _ := X.Dims()
errors := make([]float64, epochs)
for epoch := 0; epoch < epochs; epoch++ {
epochErrors := 0
for i := 0; i < rows; i++ {
x := mat.NewVecDense(X.RawRowView(i))
prediction := p.Predict(x)
if prediction != y[i] {
epochErrors++
}
p.Train(x, y[i])
}
errors[epoch] = float64(epochErrors) / float64(rows)
}
return errors
}
Activation Functions
Common activation functions and their derivatives:
// Sigmoid activation
func sigmoid(x float64) float64 {
return 1.0 / (1.0 + math.Exp(-x))
}
func sigmoidDerivative(x float64) float64 {
s := sigmoid(x)
return s * (1 - s)
}
// ReLU activation
func relu(x float64) float64 {
if x > 0 {
return x
}
return 0
}
func reluDerivative(x float64) float64 {
if x > 0 {
return 1
}
return 0
}
// Tanh activation
func tanh(x float64) float64 {
return math.Tanh(x)
}
func tanhDerivative(x float64) float64 {
t := math.Tanh(x)
return 1 - t*t
}
// Apply activation to matrix
func applyActivation(m *mat.Dense, fn func(float64) float64) *mat.Dense {
rows, cols := m.Dims()
result := mat.NewDense(rows, cols, nil)
for i := 0; i < rows; i++ {
for j := 0; j < cols; j++ {
result.Set(i, j, fn(m.At(i, j)))
}
}
return result
}
Multi-Layer Network
A simple feedforward network:
// Layer represents a single neural network layer
type Layer struct {
Weights *mat.Dense
Bias *mat.VecDense
Input *mat.Dense // Cached for backprop
Output *mat.Dense // Cached for backprop
Z *mat.Dense // Pre-activation values
}
// NeuralNetwork represents a multi-layer network
type NeuralNetwork struct {
Layers []*Layer
LearningRate float64
}
// NewNeuralNetwork creates a network with given layer sizes
func NewNeuralNetwork(sizes []int, lr float64) *NeuralNetwork {
layers := make([]*Layer, len(sizes)-1)
for i := 0; i < len(sizes)-1; i++ {
inputSize := sizes[i]
outputSize := sizes[i+1]
// Xavier initialization
scale := math.Sqrt(2.0 / float64(inputSize+outputSize))
weights := mat.NewDense(inputSize, outputSize, nil)
for r := 0; r < inputSize; r++ {
for c := 0; c < outputSize; c++ {
weights.Set(r, c, (rand.Float64()-0.5)*2*scale)
}
}
bias := mat.NewVecDense(outputSize, nil)
layers[i] = &Layer{
Weights: weights,
Bias: bias,
}
}
return &NeuralNetwork{
Layers: layers,
LearningRate: lr,
}
}
Forward Propagation
Compute network output:
// Forward performs forward propagation
func (nn *NeuralNetwork) Forward(X *mat.Dense) *mat.Dense {
current := X
for i, layer := range nn.Layers {
layer.Input = current
rows, _ := current.Dims()
_, outputSize := layer.Weights.Dims()
// Z = X @ W + b
z := mat.NewDense(rows, outputSize, nil)
z.Mul(current, layer.Weights)
// Add bias to each row
for r := 0; r < rows; r++ {
for c := 0; c < outputSize; c++ {
z.Set(r, c, z.At(r, c)+layer.Bias.AtVec(c))
}
}
layer.Z = z
// Apply activation (sigmoid for hidden, softmax for output)
if i < len(nn.Layers)-1 {
current = applyActivation(z, sigmoid)
} else {
current = softmax(z)
}
layer.Output = current
}
return current
}
// Softmax for output layer
func softmax(z *mat.Dense) *mat.Dense {
rows, cols := z.Dims()
result := mat.NewDense(rows, cols, nil)
for r := 0; r < rows; r++ {
// Find max for numerical stability
max := z.At(r, 0)
for c := 1; c < cols; c++ {
if z.At(r, c) > max {
max = z.At(r, c)
}
}
// Compute exp and sum
sum := 0.0
for c := 0; c < cols; c++ {
result.Set(r, c, math.Exp(z.At(r, c)-max))
sum += result.At(r, c)
}
// Normalize
for c := 0; c < cols; c++ {
result.Set(r, c, result.At(r, c)/sum)
}
}
return result
}
Backpropagation
Compute gradients and update weights:
// Backward performs backpropagation
func (nn *NeuralNetwork) Backward(y *mat.Dense) {
nLayers := len(nn.Layers)
rows, _ := y.Dims()
// Output layer error: dL/dZ = output - y (for softmax + cross-entropy)
outputLayer := nn.Layers[nLayers-1]
delta := mat.NewDense(rows, y.RawMatrix().Cols, nil)
delta.Sub(outputLayer.Output, y)
// Backpropagate through layers
for i := nLayers - 1; i >= 0; i-- {
layer := nn.Layers[i]
// Compute gradients
// dW = input.T @ delta
inputRows, inputCols := layer.Input.Dims()
_, deltaC := delta.Dims()
dW := mat.NewDense(inputCols, deltaC, nil)
dW.Mul(layer.Input.T(), delta)
dW.Scale(1.0/float64(rows), dW)
// dB = mean(delta, axis=0)
dB := mat.NewVecDense(deltaC, nil)
for c := 0; c < deltaC; c++ {
sum := 0.0
for r := 0; r < rows; r++ {
sum += delta.At(r, c)
}
dB.SetVec(c, sum/float64(rows))
}
// Update weights and biases
dW.Scale(nn.LearningRate, dW)
layer.Weights.Sub(layer.Weights, dW)
for c := 0; c < deltaC; c++ {
layer.Bias.SetVec(c, layer.Bias.AtVec(c)-nn.LearningRate*dB.AtVec(c))
}
// Propagate error to previous layer
if i > 0 {
prevLayer := nn.Layers[i-1]
_, prevCols := prevLayer.Output.Dims()
// delta = delta @ W.T * sigmoid'(z)
newDelta := mat.NewDense(rows, prevCols, nil)
newDelta.Mul(delta, layer.Weights.T())
// Element-wise multiply by sigmoid derivative
for r := 0; r < rows; r++ {
for c := 0; c < prevCols; c++ {
sigDeriv := sigmoidDerivative(prevLayer.Z.At(r, c))
newDelta.Set(r, c, newDelta.At(r, c)*sigDeriv)
}
}
delta = newDelta
}
}
}
Training Loop
Complete training with loss computation:
// CrossEntropyLoss computes cross-entropy loss
func CrossEntropyLoss(yPred, yTrue *mat.Dense) float64 {
rows, cols := yTrue.Dims()
loss := 0.0
for r := 0; r < rows; r++ {
for c := 0; c < cols; c++ {
if yTrue.At(r, c) > 0 {
pred := math.Max(yPred.At(r, c), 1e-15) // Avoid log(0)
loss -= yTrue.At(r, c) * math.Log(pred)
}
}
}
return loss / float64(rows)
}
// Train trains the network
func (nn *NeuralNetwork) Train(X, y *mat.Dense, epochs int, batchSize int) []float64 {
rows, _ := X.Dims()
losses := make([]float64, epochs)
for epoch := 0; epoch < epochs; epoch++ {
epochLoss := 0.0
nBatches := 0
for start := 0; start < rows; start += batchSize {
end := start + batchSize
if end > rows {
end = rows
}
// Get batch
XBatch := X.Slice(start, end, 0, X.RawMatrix().Cols).(*mat.Dense)
yBatch := y.Slice(start, end, 0, y.RawMatrix().Cols).(*mat.Dense)
// Forward and backward pass
output := nn.Forward(XBatch)
nn.Backward(yBatch)
epochLoss += CrossEntropyLoss(output, yBatch)
nBatches++
}
losses[epoch] = epochLoss / float64(nBatches)
}
return losses
}
// Predict returns class predictions
func (nn *NeuralNetwork) Predict(X *mat.Dense) []int {
output := nn.Forward(X)
rows, cols := output.Dims()
predictions := make([]int, rows)
for r := 0; r < rows; r++ {
maxIdx := 0
maxVal := output.At(r, 0)
for c := 1; c < cols; c++ {
if output.At(r, c) > maxVal {
maxVal = output.At(r, c)
maxIdx = c
}
}
predictions[r] = maxIdx
}
return predictions
}
Usage Example
func main() {
// XOR problem (simple non-linear example)
X := mat.NewDense(4, 2, []float64{
0, 0,
0, 1,
1, 0,
1, 1,
})
// One-hot encoded labels
y := mat.NewDense(4, 2, []float64{
1, 0, // Class 0
0, 1, // Class 1
0, 1, // Class 1
1, 0, // Class 0
})
// Create network: 2 inputs -> 4 hidden -> 2 outputs
nn := NewNeuralNetwork([]int{2, 4, 2}, 0.5)
// Train
losses := nn.Train(X, y, 1000, 4)
fmt.Println("Training loss (first 10 epochs):")
for i := 0; i < 10 && i < len(losses); i++ {
fmt.Printf(" Epoch %d: %.4f\n", i+1, losses[i])
}
fmt.Printf(" ...\n Epoch %d: %.4f\n", len(losses), losses[len(losses)-1])
// Predict
predictions := nn.Predict(X)
fmt.Println("\nPredictions:")
for i, p := range predictions {
fmt.Printf(" Input [%.0f, %.0f] -> Class %d\n",
X.At(i, 0), X.At(i, 1), p)
}
}
Visualizing Training Progress
Plotting loss curves helps diagnose training:
package main
import (
"image/color"
"math"
"math/rand"
"gonum.org/v1/plot"
"gonum.org/v1/plot/plotter"
"gonum.org/v1/plot/vg"
)
func main() {
rand.Seed(42)
p := plot.New()
p.Title.Text = "Neural Network Training"
p.X.Label.Text = "Epoch"
p.Y.Label.Text = "Loss"
epochs := 80
trainLoss := make(plotter.XYs, epochs)
valLoss := make(plotter.XYs, epochs)
for i := 0; i < epochs; i++ {
t := float64(i)
trainLoss[i] = plotter.XY{X: t, Y: 2.5*math.Exp(-0.05*t) + 0.1 + rand.Float64()*0.05}
valLoss[i] = plotter.XY{X: t, Y: 2.5*math.Exp(-0.04*t) + 0.15 + rand.Float64()*0.08}
}
trainLine, _ := plotter.NewLine(trainLoss)
trainLine.Color = color.RGBA{R: 66, G: 133, B: 244, A: 255}
trainLine.Width = vg.Points(2)
valLine, _ := plotter.NewLine(valLoss)
valLine.Color = color.RGBA{R: 234, G: 67, B: 53, A: 255}
valLine.Width = vg.Points(2)
p.Add(trainLine, valLine)
p.Legend.Add("Train", trainLine)
p.Legend.Add("Validation", valLine)
p.Legend.Top = true
p.Save(6*vg.Inch, 4*vg.Inch, "neural-networks.png")
}
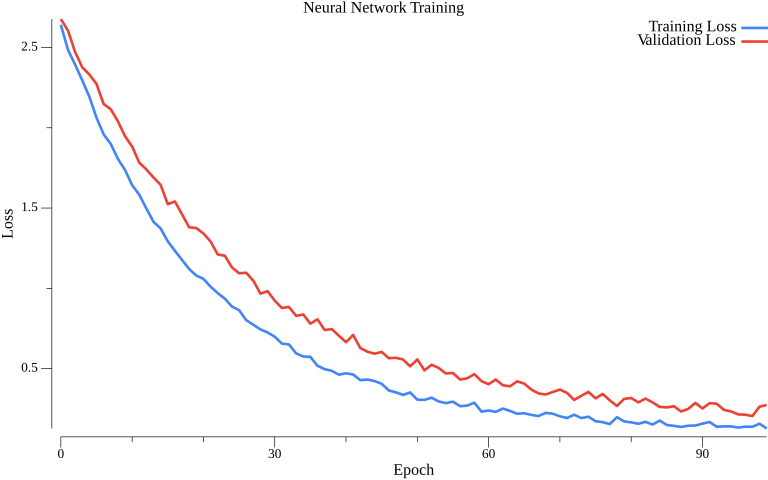
The training curve (blue) and validation curve (red) both decrease over time. The gap between them helps detect overfitting - a widening gap indicates the model memorizes training data rather than learning generalizable patterns.
Gradient Checking
Verify backpropagation implementation:
// NumericalGradient computes gradient numerically
func NumericalGradient(nn *NeuralNetwork, X, y *mat.Dense, layerIdx, i, j int, eps float64) float64 {
layer := nn.Layers[layerIdx]
original := layer.Weights.At(i, j)
// f(w + eps)
layer.Weights.Set(i, j, original+eps)
output1 := nn.Forward(X)
loss1 := CrossEntropyLoss(output1, y)
// f(w - eps)
layer.Weights.Set(i, j, original-eps)
output2 := nn.Forward(X)
loss2 := CrossEntropyLoss(output2, y)
// Restore
layer.Weights.Set(i, j, original)
return (loss1 - loss2) / (2 * eps)
}
func gradientCheck() {
nn := NewNeuralNetwork([]int{2, 3, 2}, 0.1)
X := mat.NewDense(2, 2, []float64{1, 2, 3, 4})
y := mat.NewDense(2, 2, []float64{1, 0, 0, 1})
// Compute analytical gradient via backprop
nn.Forward(X)
nn.Backward(y)
// Compare with numerical gradient
eps := 1e-5
fmt.Println("Gradient check:")
for l := 0; l < len(nn.Layers); l++ {
layer := nn.Layers[l]
rows, cols := layer.Weights.Dims()
for i := 0; i < rows && i < 2; i++ {
for j := 0; j < cols && j < 2; j++ {
numerical := NumericalGradient(nn, X, y, l, i, j, eps)
fmt.Printf(" Layer %d [%d,%d]: numerical=%.6f\n", l, i, j, numerical)
}
}
}
}
Summary
This article implemented:
- Perceptron single-layer classifier
- Activation functions with derivatives
- Forward propagation through multiple layers
- Backpropagation for gradient computation
- Training loop with cross-entropy loss
- Gradient checking for verification
Resources
Linear Algebra: Golang Series - View all articles in this series.
Note: This blog is a collection of personal notes. Making them public encourages me to think beyond the limited scope of the current problem I'm trying to solve or concept I'm implementing, and hopefully provides something useful to my team and others.
This blog post, titled: "Linear Algebra in Go: Neural Network Foundations: Linear Algebra in Go Part 9" by Craig Johnston, is licensed under a Creative Commons Attribution 4.0 International License.
