Linear Algebra in Go: Matrix Fundamentals

This article covers matrix fundamentals in Go using the gonum library: matrix creation, basic arithmetic operations, and common matrix manipulations.

Linear Algebra: Golang Series - View all articles in this series.

Previous articles in this series:

1. Linear Algebra in Go: Vectors and Basic Operations

This continues from Part 1: Vectors and Basic Operations.

Creating Matrices

Gonum’s mat.Dense is the primary matrix type:

package main

import (
    "fmt"
    "gonum.org/v1/gonum/mat"
)

func main() {
    // Create a 3x4 matrix from row-major data
    data := []float64{
        1, 2, 3, 4,
        5, 6, 7, 8,
        9, 10, 11, 12,
    }
    A := mat.NewDense(3, 4, data)

    fmt.Println("Matrix A (3x4):")
    fmt.Printf("%v\n", mat.Formatted(A, mat.Prefix("  ")))

    // Get dimensions
    rows, cols := A.Dims()
    fmt.Printf("Dimensions: %d x %d\n", rows, cols)

    // Access elements (0-indexed)
    fmt.Printf("A[1,2] = %.2f\n", A.At(1, 2))
}

Output:

Matrix A (3x4):
  [1  2  3  4]
  [5  6  7  8]
  [9  10  11  12]
Dimensions: 3 x 4
A[1,2] = 7.00

Special Matrices

Identity Matrix

func identityMatrix() {
    // Create 4x4 identity matrix
    I := mat.NewDiagDense(4, []float64{1, 1, 1, 1})
    fmt.Println("Identity matrix:")
    fmt.Printf("%v\n", mat.Formatted(I))
}

Zero Matrix

func zeroMatrix() {
    // Create 3x3 zero matrix
    Z := mat.NewDense(3, 3, nil)  // nil initializes to zeros
    fmt.Println("Zero matrix:")
    fmt.Printf("%v\n", mat.Formatted(Z))
}

Diagonal Matrix

func diagonalMatrix() {
    // Create diagonal matrix
    diag := []float64{2, 3, 5, 7}
    D := mat.NewDiagDense(4, diag)
    fmt.Println("Diagonal matrix:")
    fmt.Printf("%v\n", mat.Formatted(D))
}

Matrix Arithmetic

Addition and Subtraction

func matrixAddition() {
    A := mat.NewDense(2, 2, []float64{1, 2, 3, 4})
    B := mat.NewDense(2, 2, []float64{5, 6, 7, 8})

    // Addition
    sum := mat.NewDense(2, 2, nil)
    sum.Add(A, B)
    fmt.Println("A + B:")
    fmt.Printf("%v\n", mat.Formatted(sum))

    // Subtraction
    diff := mat.NewDense(2, 2, nil)
    diff.Sub(A, B)
    fmt.Println("A - B:")
    fmt.Printf("%v\n", mat.Formatted(diff))
}

Output:

A + B:
[6  8]
[10  12]
A - B:
[-4  -4]
[-4  -4]

Scalar Multiplication

func scalarMultiplication() {
    A := mat.NewDense(2, 3, []float64{1, 2, 3, 4, 5, 6})
    scalar := 2.5

    result := mat.NewDense(2, 3, nil)
    result.Scale(scalar, A)

    fmt.Printf("%.1f * A:\n", scalar)
    fmt.Printf("%v\n", mat.Formatted(result))
}

Matrix Multiplication

func matrixMultiplication() {
    // A: 2x3
    A := mat.NewDense(2, 3, []float64{
        1, 2, 3,
        4, 5, 6,
    })

    // B: 3x2
    B := mat.NewDense(3, 2, []float64{
        7, 8,
        9, 10,
        11, 12,
    })

    // C = A * B (2x2)
    var C mat.Dense
    C.Mul(A, B)

    fmt.Println("A (2x3):")
    fmt.Printf("%v\n", mat.Formatted(A))
    fmt.Println("B (3x2):")
    fmt.Printf("%v\n", mat.Formatted(B))
    fmt.Println("A * B (2x2):")
    fmt.Printf("%v\n", mat.Formatted(&C))
}

Output:

A (2x3):
[1  2  3]
[4  5  6]
B (3x2):
[7   8]
[9   10]
[11  12]
A * B (2x2):
[58   64]
[139  154]

Element-wise Operations

func elementWiseOperations() {
    A := mat.NewDense(2, 2, []float64{1, 2, 3, 4})
    B := mat.NewDense(2, 2, []float64{5, 6, 7, 8})

    // Element-wise multiplication (Hadamard product)
    result := mat.NewDense(2, 2, nil)
    result.MulElem(A, B)

    fmt.Println("A ⊙ B (element-wise):")
    fmt.Printf("%v\n", mat.Formatted(result))

    // Element-wise division
    result.DivElem(A, B)
    fmt.Println("A ⊘ B (element-wise division):")
    fmt.Printf("%v\n", mat.Formatted(result))
}

Visualizing Matrix Transformations

Matrices represent linear transformations. Here’s how a matrix transforms the unit square:

package main

import (
    "image/color"

    "gonum.org/v1/gonum/mat"
    "gonum.org/v1/plot"
    "gonum.org/v1/plot/plotter"
    "gonum.org/v1/plot/vg"
)

func main() {
    p := plot.New()
    p.Title.Text = "Matrix Transformation"
    p.X.Min, p.X.Max = -1, 5
    p.Y.Min, p.Y.Max = -1, 4

    // Unit square vertices
    square := [][]float64{{0, 0}, {1, 0}, {1, 1}, {0, 1}, {0, 0}}

    // Transformation matrix
    A := mat.NewDense(2, 2, []float64{2, 1, 0.5, 1.5})

    // Original square (blue)
    origPts := make(plotter.XYs, len(square))
    for i, pt := range square {
        origPts[i] = plotter.XY{X: pt[0], Y: pt[1]}
    }
    origLine, _ := plotter.NewLine(origPts)
    origLine.Color = color.RGBA{R: 66, G: 133, B: 244, A: 255}
    origLine.Width = vg.Points(2)

    // Transformed square (red)
    transPts := make(plotter.XYs, len(square))
    for i, pt := range square {
        v := mat.NewVecDense(2, pt)
        var result mat.VecDense
        result.MulVec(A, v)
        transPts[i] = plotter.XY{X: result.AtVec(0), Y: result.AtVec(1)}
    }
    transLine, _ := plotter.NewLine(transPts)
    transLine.Color = color.RGBA{R: 234, G: 67, B: 53, A: 255}
    transLine.Width = vg.Points(2)

    p.Add(origLine, transLine)
    p.Save(6*vg.Inch, 5*vg.Inch, "matrix-transform.png")
}

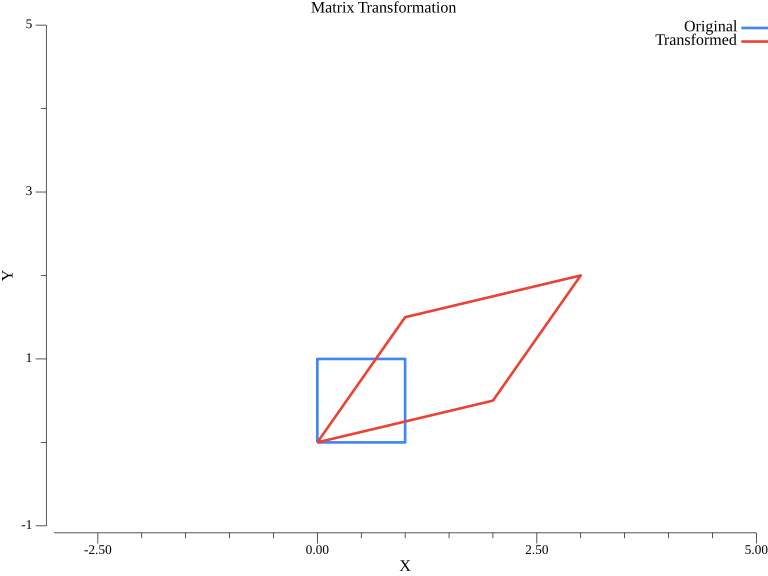
The blue unit square is transformed by matrix A into the red parallelogram. This visualizes how matrices stretch, shear, and rotate space.

Matrix Transposition

func matrixTranspose() {
    A := mat.NewDense(2, 3, []float64{
        1, 2, 3,
        4, 5, 6,
    })

    // Transpose
    var AT mat.Dense
    AT.CloneFrom(A.T())

    fmt.Println("A:")
    fmt.Printf("%v\n", mat.Formatted(A))
    fmt.Println("A^T:")
    fmt.Printf("%v\n", mat.Formatted(&AT))

    // Note: A.T() returns a view, not a copy
    // Use CloneFrom for a separate matrix
}

Output:

A:
[1  2  3]
[4  5  6]
A^T:
[1  4]
[2  5]
[3  6]

Matrix Slicing and Submatrices

func matrixSlicing() {
    A := mat.NewDense(4, 4, []float64{
        1, 2, 3, 4,
        5, 6, 7, 8,
        9, 10, 11, 12,
        13, 14, 15, 16,
    })

    fmt.Println("Original matrix A:")
    fmt.Printf("%v\n", mat.Formatted(A))

    // Extract a row
    row := A.RowView(1)  // Second row
    fmt.Printf("Row 1: %v\n", mat.Formatted(row.T()))

    // Extract a column
    col := A.ColView(2)  // Third column
    fmt.Printf("Column 2: %v\n", mat.Formatted(col))

    // Extract a submatrix (rows 1-2, cols 1-2)
    sub := A.Slice(1, 3, 1, 3).(*mat.Dense)
    fmt.Println("Submatrix [1:3, 1:3]:")
    fmt.Printf("%v\n", mat.Formatted(sub))
}

Modifying Matrices

func modifyMatrix() {
    A := mat.NewDense(3, 3, nil)

    // Set individual elements
    A.Set(0, 0, 1)
    A.Set(1, 1, 2)
    A.Set(2, 2, 3)

    fmt.Println("After setting diagonal:")
    fmt.Printf("%v\n", mat.Formatted(A))

    // Set a row
    A.SetRow(0, []float64{7, 8, 9})
    fmt.Println("After setting row 0:")
    fmt.Printf("%v\n", mat.Formatted(A))

    // Set a column
    A.SetCol(2, []float64{10, 20, 30})
    fmt.Println("After setting column 2:")
    fmt.Printf("%v\n", mat.Formatted(A))
}

Matrix Properties

func matrixProperties() {
    A := mat.NewDense(3, 3, []float64{
        1, 2, 3,
        4, 5, 6,
        7, 8, 9,
    })

    // Trace (sum of diagonal)
    trace := mat.Trace(A)
    fmt.Printf("Trace: %.2f\n", trace)

    // Sum of all elements
    sum := mat.Sum(A)
    fmt.Printf("Sum of all elements: %.2f\n", sum)

    // Frobenius norm
    frobNorm := mat.Norm(A, 2)
    fmt.Printf("Frobenius norm: %.4f\n", frobNorm)
}

Output:

Trace: 15.00
Sum of all elements: 45.00
Frobenius norm: 16.8819

Sparse Matrices

For matrices with many zeros, use sparse representations:

import "gonum.org/v1/gonum/mat"

func sparseMatrixExample() {
    // Create a sparse matrix using DOK (Dictionary of Keys)
    // then convert to dense if needed
    data := map[int]map[int]float64{
        0: {0: 1, 2: 2},
        1: {1: 3},
        2: {0: 4, 2: 5},
    }

    // Create dense from sparse data
    A := mat.NewDense(3, 3, nil)
    for i, row := range data {
        for j, val := range row {
            A.Set(i, j, val)
        }
    }

    fmt.Println("Sparse matrix as dense:")
    fmt.Printf("%v\n", mat.Formatted(A))
}

Complete Working Example

package main

import (
    "fmt"
    "gonum.org/v1/gonum/mat"
)

func main() {
    fmt.Println("=== Matrix Fundamentals in Go ===\n")

    // Create matrices
    A := mat.NewDense(2, 3, []float64{1, 2, 3, 4, 5, 6})
    B := mat.NewDense(3, 2, []float64{7, 8, 9, 10, 11, 12})

    fmt.Println("Matrix A:")
    fmt.Printf("%v\n\n", mat.Formatted(A, mat.Prefix("  ")))

    fmt.Println("Matrix B:")
    fmt.Printf("%v\n\n", mat.Formatted(B, mat.Prefix("  ")))

    // Multiplication
    var C mat.Dense
    C.Mul(A, B)
    fmt.Println("A * B:")
    fmt.Printf("%v\n\n", mat.Formatted(&C, mat.Prefix("  ")))

    // Transpose
    var AT mat.Dense
    AT.CloneFrom(A.T())
    fmt.Println("A^T:")
    fmt.Printf("%v\n", mat.Formatted(&AT, mat.Prefix("  ")))
}

Summary

This article covered:

• Creating matrices with mat.Dense
• Special matrices: identity, zero, diagonal
• Matrix arithmetic: addition, subtraction, multiplication
• Element-wise operations: Hadamard product
• Transposition: A.T()
• Slicing and submatrices
• Matrix properties: trace, sum, norm

Resources

• Gonum mat Package
• Matrix Operations in Python

Linear Algebra: Golang Series - View all articles in this series.

This blog post, titled: "Linear Algebra in Go: Matrix Fundamentals: Linear Algebra in Go Part 2" by Craig Johnston, is licensed under a Creative Commons Attribution 4.0 International License.