Linear Algebra Linear Algebra: Golang Golang High Performance Data Science

Linear Algebra in Go: High-Performance Computing

Linear Algebra in Go Part 10

Posted by Craig Johnston on Wednesday, May 25, 2022

This final article in the series covers high-performance computing techniques for linear algebra in Go: BLAS/LAPACK integration, parallel operations, memory optimization, and benchmarking.

Linear Algebra: Golang Series - View all articles in this series.

Previous articles in this series:

  1. Linear Algebra in Go: Vectors and Basic Operations
  2. Linear Algebra in Go: Matrix Fundamentals
  3. Linear Algebra in Go: Solving Linear Systems
  4. Linear Algebra in Go: Eigenvalue Problems
  5. Linear Algebra in Go: SVD and Decompositions
  6. Linear Algebra in Go: Statistics and Data Analysis
  7. Linear Algebra in Go: Building a Regression Library
  8. Linear Algebra in Go: PCA Implementation
  9. Linear Algebra in Go: Neural Network Foundations

This continues from Part 9: Neural Network Foundations.

BLAS and LAPACK

Gonum uses BLAS (Basic Linear Algebra Subprograms) under the hood. You can choose between pure Go and optimized C implementations.

Using OpenBLAS

For better performance, install OpenBLAS and use the netlib bindings:

# macOS
brew install openblas

# Ubuntu/Debian
apt-get install libopenblas-dev

# Build with netlib
go build -tags=netlib

Then import the netlib BLAS:

package main

import (
    "gonum.org/v1/gonum/blas/blas64"
    "gonum.org/v1/netlib/blas/netlib"
)

func init() {
    // Use OpenBLAS instead of native Go
    blas64.Use(netlib.Implementation{})
}

BLAS Levels

import "gonum.org/v1/gonum/blas/blas64"

// Level 1: Vector operations
func blasLevel1() {
    x := blas64.Vector{N: 4, Inc: 1, Data: []float64{1, 2, 3, 4}}
    y := blas64.Vector{N: 4, Inc: 1, Data: []float64{5, 6, 7, 8}}

    // Dot product
    dot := blas64.Dot(x, y)
    fmt.Printf("Dot product: %.2f\n", dot)

    // Norm
    norm := blas64.Nrm2(x)
    fmt.Printf("L2 norm: %.2f\n", norm)

    // Scale: y = alpha * x + y
    blas64.Axpy(2.0, x, y)
    fmt.Printf("After axpy: %v\n", y.Data)
}

// Level 2: Matrix-vector operations
func blasLevel2() {
    A := blas64.General{
        Rows:   2,
        Cols:   3,
        Stride: 3,
        Data:   []float64{1, 2, 3, 4, 5, 6},
    }
    x := blas64.Vector{N: 3, Inc: 1, Data: []float64{1, 1, 1}}
    y := blas64.Vector{N: 2, Inc: 1, Data: []float64{0, 0}}

    // y = alpha * A * x + beta * y
    blas64.Gemv(blas.NoTrans, 1.0, A, x, 0.0, y)
    fmt.Printf("A * x = %v\n", y.Data)
}

// Level 3: Matrix-matrix operations
func blasLevel3() {
    A := blas64.General{Rows: 2, Cols: 3, Stride: 3, Data: []float64{1, 2, 3, 4, 5, 6}}
    B := blas64.General{Rows: 3, Cols: 2, Stride: 2, Data: []float64{1, 2, 3, 4, 5, 6}}
    C := blas64.General{Rows: 2, Cols: 2, Stride: 2, Data: make([]float64, 4)}

    // C = alpha * A * B + beta * C
    blas64.Gemm(blas.NoTrans, blas.NoTrans, 1.0, A, B, 0.0, C)
    fmt.Printf("A * B = %v\n", C.Data)
}

Parallel Operations

Using Goroutines for Row Operations

import "sync"

// ParallelRowOp applies a function to each row in parallel
func ParallelRowOp(A *mat.Dense, op func(row []float64)) {
    rows, cols := A.Dims()
    var wg sync.WaitGroup
    wg.Add(rows)

    for i := 0; i < rows; i++ {
        go func(rowIdx int) {
            defer wg.Done()
            row := make([]float64, cols)
            mat.Row(row, rowIdx, A)
            op(row)
            A.SetRow(rowIdx, row)
        }(i)
    }

    wg.Wait()
}

// Example: normalize each row
func normalizeRows(A *mat.Dense) {
    ParallelRowOp(A, func(row []float64) {
        sum := 0.0
        for _, v := range row {
            sum += v * v
        }
        norm := math.Sqrt(sum)
        if norm > 0 {
            for i := range row {
                row[i] /= norm
            }
        }
    })
}

Parallel Matrix Multiplication with Tiling

// ParallelMatMul performs tiled parallel matrix multiplication
func ParallelMatMul(A, B *mat.Dense, tileSize int) *mat.Dense {
    rowsA, colsA := A.Dims()
    rowsB, colsB := B.Dims()

    if colsA != rowsB {
        panic("dimension mismatch")
    }

    C := mat.NewDense(rowsA, colsB, nil)

    // Number of tiles
    tilesI := (rowsA + tileSize - 1) / tileSize
    tilesJ := (colsB + tileSize - 1) / tileSize
    tilesK := (colsA + tileSize - 1) / tileSize

    var wg sync.WaitGroup
    var mu sync.Mutex

    for ti := 0; ti < tilesI; ti++ {
        for tj := 0; tj < tilesJ; tj++ {
            wg.Add(1)
            go func(ti, tj int) {
                defer wg.Done()

                iStart := ti * tileSize
                iEnd := min(iStart+tileSize, rowsA)
                jStart := tj * tileSize
                jEnd := min(jStart+tileSize, colsB)

                // Local accumulator
                local := mat.NewDense(iEnd-iStart, jEnd-jStart, nil)

                for tk := 0; tk < tilesK; tk++ {
                    kStart := tk * tileSize
                    kEnd := min(kStart+tileSize, colsA)

                    // Multiply tile
                    ATile := A.Slice(iStart, iEnd, kStart, kEnd)
                    BTile := B.Slice(kStart, kEnd, jStart, jEnd)

                    var temp mat.Dense
                    temp.Mul(ATile, BTile)
                    local.Add(local, &temp)
                }

                // Write to result
                mu.Lock()
                for i := iStart; i < iEnd; i++ {
                    for j := jStart; j < jEnd; j++ {
                        C.Set(i, j, C.At(i, j)+local.At(i-iStart, j-jStart))
                    }
                }
                mu.Unlock()
            }(ti, tj)
        }
    }

    wg.Wait()
    return C
}

func min(a, b int) int {
    if a < b {
        return a
    }
    return b
}

Worker Pool Pattern

// MatrixWorkerPool manages parallel matrix operations
type MatrixWorkerPool struct {
    workers int
    tasks   chan func()
    wg      sync.WaitGroup
}

func NewMatrixWorkerPool(workers int) *MatrixWorkerPool {
    pool := &MatrixWorkerPool{
        workers: workers,
        tasks:   make(chan func(), workers*2),
    }

    for i := 0; i < workers; i++ {
        go pool.worker()
    }

    return pool
}

func (p *MatrixWorkerPool) worker() {
    for task := range p.tasks {
        task()
        p.wg.Done()
    }
}

func (p *MatrixWorkerPool) Submit(task func()) {
    p.wg.Add(1)
    p.tasks <- task
}

func (p *MatrixWorkerPool) Wait() {
    p.wg.Wait()
}

func (p *MatrixWorkerPool) Close() {
    close(p.tasks)
}

// Usage
func parallelSVD(matrices []*mat.Dense) []*mat.SVD {
    pool := NewMatrixWorkerPool(runtime.NumCPU())
    defer pool.Close()

    results := make([]*mat.SVD, len(matrices))
    var mu sync.Mutex

    for i, m := range matrices {
        idx := i
        matrix := m
        pool.Submit(func() {
            var svd mat.SVD
            svd.Factorize(matrix, mat.SVDThin)

            mu.Lock()
            results[idx] = &svd
            mu.Unlock()
        })
    }

    pool.Wait()
    return results
}

Memory Optimization

Pre-allocated Workspaces

// Workspace holds pre-allocated memory for operations
type Workspace struct {
    tempA *mat.Dense
    tempB *mat.Dense
    tempV *mat.VecDense
}

func NewWorkspace(maxRows, maxCols int) *Workspace {
    return &Workspace{
        tempA: mat.NewDense(maxRows, maxCols, nil),
        tempB: mat.NewDense(maxRows, maxCols, nil),
        tempV: mat.NewVecDense(maxRows, nil),
    }
}

// MultiplyInPlace uses pre-allocated memory
func (w *Workspace) MultiplyInPlace(A, B, result *mat.Dense) {
    result.Mul(A, B)
}

// ChainMultiply multiplies A * B * C using workspace
func (w *Workspace) ChainMultiply(A, B, C *mat.Dense) *mat.Dense {
    rowsA, _ := A.Dims()
    _, colsB := B.Dims()
    _, colsC := C.Dims()

    // Resize temp if needed
    w.tempA.Reset()
    w.tempA.ReuseAs(rowsA, colsB)

    w.tempA.Mul(A, B)

    result := mat.NewDense(rowsA, colsC, nil)
    result.Mul(w.tempA, C)

    return result
}

Memory Pool for Matrices

import "sync"

// MatrixPool manages reusable matrix allocations
type MatrixPool struct {
    pools map[string]*sync.Pool
    mu    sync.RWMutex
}

func NewMatrixPool() *MatrixPool {
    return &MatrixPool{
        pools: make(map[string]*sync.Pool),
    }
}

func (p *MatrixPool) getKey(rows, cols int) string {
    return fmt.Sprintf("%d_%d", rows, cols)
}

func (p *MatrixPool) Get(rows, cols int) *mat.Dense {
    key := p.getKey(rows, cols)

    p.mu.RLock()
    pool, exists := p.pools[key]
    p.mu.RUnlock()

    if !exists {
        p.mu.Lock()
        pool = &sync.Pool{
            New: func() interface{} {
                return mat.NewDense(rows, cols, nil)
            },
        }
        p.pools[key] = pool
        p.mu.Unlock()
    }

    m := pool.Get().(*mat.Dense)
    m.Zero()
    return m
}

func (p *MatrixPool) Put(m *mat.Dense) {
    rows, cols := m.Dims()
    key := p.getKey(rows, cols)

    p.mu.RLock()
    pool, exists := p.pools[key]
    p.mu.RUnlock()

    if exists {
        pool.Put(m)
    }
}

Avoiding Allocations in Hot Paths

// Bad: allocates on every call
func dotProductBad(a, b []float64) float64 {
    result := make([]float64, len(a))  // Allocation!
    for i := range a {
        result[i] = a[i] * b[i]
    }
    sum := 0.0
    for _, v := range result {
        sum += v
    }
    return sum
}

// Good: no allocation
func dotProductGood(a, b []float64) float64 {
    sum := 0.0
    for i := range a {
        sum += a[i] * b[i]
    }
    return sum
}

// Good: reuse slice with Reset
func (r *Result) ComputeNorms(vectors []*mat.VecDense) {
    for _, v := range vectors {
        norm := mat.Norm(v, 2)
        r.norms = append(r.norms, norm)
    }
}

// Reset before reuse
func (r *Result) Reset() {
    r.norms = r.norms[:0]  // Reuse backing array
}

Benchmarking

Basic Benchmarks

import "testing"

func BenchmarkMatMul(b *testing.B) {
    sizes := []int{100, 500, 1000}

    for _, n := range sizes {
        A := mat.NewDense(n, n, nil)
        B := mat.NewDense(n, n, nil)

        // Initialize with random data
        for i := 0; i < n; i++ {
            for j := 0; j < n; j++ {
                A.Set(i, j, rand.Float64())
                B.Set(i, j, rand.Float64())
            }
        }

        b.Run(fmt.Sprintf("size_%d", n), func(b *testing.B) {
            var C mat.Dense
            b.ResetTimer()
            for i := 0; i < b.N; i++ {
                C.Mul(A, B)
            }
        })
    }
}

func BenchmarkSVD(b *testing.B) {
    sizes := []int{50, 100, 200}

    for _, n := range sizes {
        A := mat.NewDense(n, n, nil)
        for i := 0; i < n; i++ {
            for j := 0; j < n; j++ {
                A.Set(i, j, rand.Float64())
            }
        }

        b.Run(fmt.Sprintf("size_%d", n), func(b *testing.B) {
            b.ResetTimer()
            for i := 0; i < b.N; i++ {
                var svd mat.SVD
                svd.Factorize(A, mat.SVDThin)
            }
        })
    }
}

Comparing Implementations

func BenchmarkParallelVsSequential(b *testing.B) {
    n := 1000
    A := mat.NewDense(n, n, nil)
    B := mat.NewDense(n, n, nil)

    for i := 0; i < n; i++ {
        for j := 0; j < n; j++ {
            A.Set(i, j, rand.Float64())
            B.Set(i, j, rand.Float64())
        }
    }

    b.Run("sequential", func(b *testing.B) {
        var C mat.Dense
        for i := 0; i < b.N; i++ {
            C.Mul(A, B)
        }
    })

    b.Run("parallel_tile64", func(b *testing.B) {
        for i := 0; i < b.N; i++ {
            ParallelMatMul(A, B, 64)
        }
    })

    b.Run("parallel_tile128", func(b *testing.B) {
        for i := 0; i < b.N; i++ {
            ParallelMatMul(A, B, 128)
        }
    })
}

Memory Profiling

func BenchmarkMemoryAllocation(b *testing.B) {
    n := 500

    b.Run("without_pool", func(b *testing.B) {
        b.ReportAllocs()
        for i := 0; i < b.N; i++ {
            A := mat.NewDense(n, n, nil)
            B := mat.NewDense(n, n, nil)
            var C mat.Dense
            C.Mul(A, B)
        }
    })

    pool := NewMatrixPool()

    b.Run("with_pool", func(b *testing.B) {
        b.ReportAllocs()
        for i := 0; i < b.N; i++ {
            A := pool.Get(n, n)
            B := pool.Get(n, n)
            var C mat.Dense
            C.Mul(A, B)
            pool.Put(A)
            pool.Put(B)
        }
    })
}

Visualizing Performance

Benchmarking different implementations helps make informed decisions:

package main

import (
    "image/color"

    "gonum.org/v1/plot"
    "gonum.org/v1/plot/plotter"
    "gonum.org/v1/plot/vg"
)

func main() {
    p := plot.New()
    p.Title.Text = "Matrix Multiplication Performance"
    p.Y.Label.Text = "Time (ms)"

    sizes := []string{"100", "500", "1000"}
    goTimes := []float64{0.5, 15, 120}
    blasTimes := []float64{0.3, 8, 55}

    w := vg.Points(25)

    goBar, _ := plotter.NewBarChart(plotter.Values(goTimes), w)
    goBar.Color = color.RGBA{R: 66, G: 133, B: 244, A: 255}
    goBar.Offset = -w / 2

    blasBar, _ := plotter.NewBarChart(plotter.Values(blasTimes), w)
    blasBar.Color = color.RGBA{R: 52, G: 168, B: 83, A: 255}
    blasBar.Offset = w / 2

    p.Add(goBar, blasBar)
    p.Legend.Add("Pure Go", goBar)
    p.Legend.Add("OpenBLAS", blasBar)
    p.Legend.Top = true
    p.NominalX(sizes...)

    p.Save(6*vg.Inch, 4*vg.Inch, "hpc.png")
}

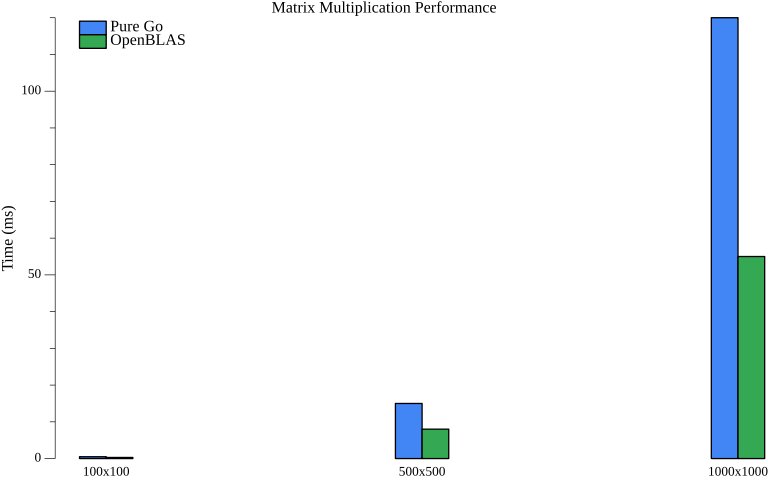
Performance comparison between pure Go and OpenBLAS implementations

The chart compares pure Go implementation (blue) with OpenBLAS-accelerated operations (green). OpenBLAS provides significant speedups, especially for larger matrices where optimized BLAS routines can leverage SIMD instructions and cache-efficient algorithms.

Performance Tips

1. Choose the Right Data Structure

// Use SymDense for symmetric matrices
sym := mat.NewSymDense(n, data)  // Half the memory

// Use TriDense for triangular matrices
tri := mat.NewTriDense(n, mat.Upper, data)

// Use DiagDense for diagonal matrices
diag := mat.NewDiagDense(n, diagData)

// Use Sparse matrices for sparse data
// (gonum/sparse package)

2. Batch Operations

// Bad: many small operations
for i := 0; i < 1000; i++ {
    v := mat.NewVecDense(n, data[i])
    result[i] = mat.Norm(v, 2)
}

// Good: single large operation
allData := mat.NewDense(1000, n, flatData)
for i := 0; i < 1000; i++ {
    row := allData.RowView(i)
    result[i] = mat.Norm(row, 2)
}

3. Leverage SIMD via BLAS

// These operations use optimized BLAS routines
var result mat.Dense
result.Mul(A, B)        // Uses DGEMM
result.Add(A, B)        // Vectorized
mat.Dot(v1, v2)         // Uses DDOT

Summary

Go with gonum provides a capable platform for numerical computing. For production workloads, use optimized BLAS implementations and leverage Go’s concurrency primitives for parallel operations.

Resources

Linear Algebra: Golang Series - View all articles in this series.

Note: This blog is a collection of personal notes. Making them public encourages me to think beyond the limited scope of the current problem I'm trying to solve or concept I'm implementing, and hopefully provides something useful to my team and others.

This blog post, titled: "Linear Algebra in Go: High-Performance Computing: Linear Algebra in Go Part 10" by Craig Johnston, is licensed under a Creative Commons Attribution 4.0 International License. Creative Commons License

FEATURED TAGS
ai apache nifi blockchain data data science development devops docker elasticsearch golang ingress iot json kubectl kubefwd kubernetes linear algebra linear algebra: golang linear algebra: python machine learning math matrices mcp microservices python raspberry pi security utils
RELATED