Linear Algebra in Go: Eigenvalue Problems

This article covers eigenvalue problems in Go using the gonum library. Eigenvalues and eigenvectors are fundamental to many algorithms including PCA, spectral clustering, and dynamical systems analysis.

Linear Algebra: Golang Series - View all articles in this series.

Previous articles in this series:

This continues from Part 3: Solving Linear Systems.

Computing Eigenvalues and Eigenvectors

Use mat.Eigen for eigenvalue decomposition:

package main

import (
    "fmt"
    "gonum.org/v1/gonum/mat"
)

func main() {
    A := mat.NewDense(3, 3, []float64{
        4, 2, 2,
        2, 5, 1,
        2, 1, 6,
    })

    // Compute eigendecomposition
    var eig mat.Eigen
    ok := eig.Factorize(A, mat.EigenRight)
    if !ok {
        fmt.Println("Eigendecomposition failed")
        return
    }

    // Get eigenvalues (may be complex)
    eigenvalues := eig.Values(nil)
    fmt.Println("Eigenvalues:")
    for i, ev := range eigenvalues {
        fmt.Printf("  λ%d = %.4f + %.4fi\n", i+1, real(ev), imag(ev))
    }

    // Get eigenvectors
    var vectors mat.CDense
    eig.VectorsTo(&vectors)
    fmt.Println("\nEigenvectors (columns):")
    rows, cols := vectors.Dims()
    for i := 0; i < rows; i++ {
        for j := 0; j < cols; j++ {
            v := vectors.At(i, j)
            fmt.Printf("  (%.4f + %.4fi)", real(v), imag(v))
        }
        fmt.Println()
    }
}

Symmetric Matrices

For symmetric matrices, use mat.EigenSym for better performance and guaranteed real eigenvalues:

func symmetricEigen() {
    // Symmetric positive-definite matrix
    A := mat.NewSymDense(3, []float64{
        4, 2, 2,
        2, 5, 1,
        2, 1, 6,
    })

    var eig mat.EigenSym
    ok := eig.Factorize(A, true)  // true = compute eigenvectors
    if !ok {
        fmt.Println("Eigendecomposition failed")
        return
    }

    // Eigenvalues (guaranteed real for symmetric matrices)
    eigenvalues := eig.Values(nil)
    fmt.Println("Eigenvalues:")
    for i, ev := range eigenvalues {
        fmt.Printf("  λ%d = %.4f\n", i+1, ev)
    }

    // Eigenvectors (orthonormal for symmetric matrices)
    var vectors mat.Dense
    eig.VectorsTo(&vectors)
    fmt.Println("\nEigenvectors:")
    fmt.Printf("%v\n", mat.Formatted(&vectors))
}

Geometric Interpretation

Eigenvectors are special directions that remain unchanged (except for scaling) under the linear transformation. Here’s a visualization using gonum/plot:

package main

import (
    "image/color"
    "math"

    "gonum.org/v1/gonum/mat"
    "gonum.org/v1/plot"
    "gonum.org/v1/plot/plotter"
    "gonum.org/v1/plot/vg"
)

func main() {
    // Matrix with eigenvalues 3 and 1
    A := mat.NewDense(2, 2, []float64{2, 1, 1, 2})

    // Compute eigenvectors
    var eig mat.EigenSym
    eig.Factorize(mat.NewSymDense(2, []float64{2, 1, 1, 2}), true)
    eigenvalues := eig.Values(nil)
    var vectors mat.Dense
    eig.VectorsTo(&vectors)

    p := plot.New()
    p.Title.Text = "Eigenvectors: Scaled but Not Rotated"
    p.X.Label.Text = "X"
    p.Y.Label.Text = "Y"
    p.X.Min, p.X.Max = -3, 3
    p.Y.Min, p.Y.Max = -3, 3

    // Draw each eigenvector and its transformation
    colors := []color.RGBA{
        {R: 66, G: 133, B: 244, A: 255},  // Blue
        {R: 234, G: 67, B: 53, A: 255},   // Red
    }

    for i := 0; i < 2; i++ {
        v := []float64{vectors.At(0, i), vectors.At(1, i)}
        lambda := eigenvalues[i]

        // Original eigenvector
        drawArrow(p, 0, 0, v[0], v[1], colors[i])

        // Transformed: A*v = lambda*v (scaled version)
        drawArrow(p, 0, 0, lambda*v[0], lambda*v[1],
            color.RGBA{R: colors[i].R, G: colors[i].G, B: colors[i].B, A: 128})
    }

    p.Save(6*vg.Inch, 6*vg.Inch, "eigenvalues-geometric.png")
}

func drawArrow(p *plot.Plot, x1, y1, x2, y2 float64, c color.Color) {
    pts := plotter.XYs{{X: x1, Y: y1}, {X: x2, Y: y2}}
    line, _ := plotter.NewLine(pts)
    line.Color = c
    line.Width = vg.Points(2)
    p.Add(line)

    // Arrowhead
    angle := math.Atan2(y2-y1, x2-x1)
    arrowLen := 0.15
    ax1 := x2 - arrowLen*math.Cos(angle-math.Pi/6)
    ay1 := y2 - arrowLen*math.Sin(angle-math.Pi/6)
    ax2 := x2 - arrowLen*math.Cos(angle+math.Pi/6)
    ay2 := y2 - arrowLen*math.Sin(angle+math.Pi/6)

    arrow1, _ := plotter.NewLine(plotter.XYs{{X: x2, Y: y2}, {X: ax1, Y: ay1}})
    arrow1.Color = c
    arrow1.Width = vg.Points(2)
    arrow2, _ := plotter.NewLine(plotter.XYs{{X: x2, Y: y2}, {X: ax2, Y: ay2}})
    arrow2.Color = c
    arrow2.Width = vg.Points(2)
    p.Add(arrow1, arrow2)
}

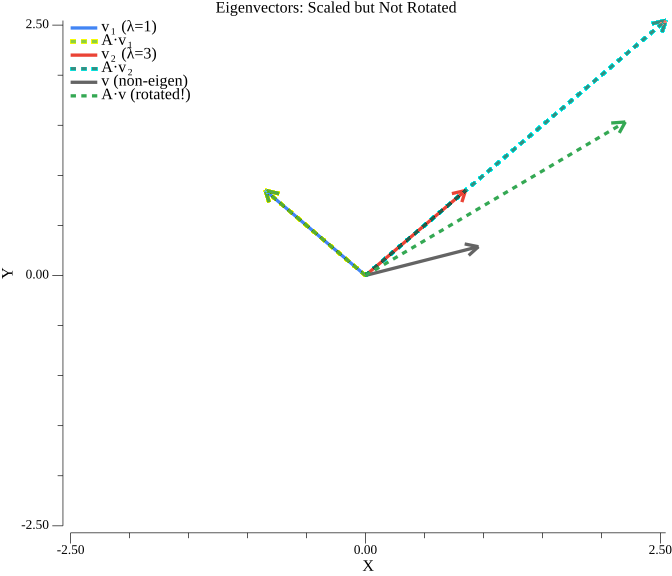
Geometric interpretation of eigenvalues - eigenvectors are scaled but not rotated

The solid arrows show eigenvectors, and the faded arrows show the result after transformation by matrix A. Notice that eigenvectors only get scaled (by their eigenvalue λ), not rotated. Non-eigenvectors would both rotate and scale.

Verifying Eigenvalue Properties

Verify that eigenvectors satisfy $\boldsymbol{A}\vec{v} = \lambda\vec{v}$:

func verifyEigenproperties() {
    A := mat.NewSymDense(2, []float64{3, 1, 1, 3})

    var eig mat.EigenSym
    eig.Factorize(A, true)

    eigenvalues := eig.Values(nil)
    var vectors mat.Dense
    eig.VectorsTo(&vectors)

    fmt.Println("Verification: A*v = λ*v")
    for i := 0; i < 2; i++ {
        // Extract eigenvector
        v := mat.NewVecDense(2, nil)
        mat.Col(v.RawVector().Data, i, &vectors)

        // Compute A*v
        var Av mat.VecDense
        Av.MulVec(A, v)

        // Compute λ*v
        lambdaV := mat.NewVecDense(2, nil)
        lambdaV.ScaleVec(eigenvalues[i], v)

        fmt.Printf("\nEigenvector %d (λ = %.4f):\n", i+1, eigenvalues[i])
        fmt.Printf("  A*v  = [%.4f, %.4f]\n", Av.AtVec(0), Av.AtVec(1))
        fmt.Printf("  λ*v  = [%.4f, %.4f]\n", lambdaV.AtVec(0), lambdaV.AtVec(1))
    }
}

Power Iteration

Implement power iteration to find the dominant eigenvalue:

func powerIteration(A *mat.Dense, maxIter int, tol float64) (float64, *mat.VecDense) {
    n, _ := A.Dims()

    // Start with random vector
    v := mat.NewVecDense(n, nil)
    for i := 0; i < n; i++ {
        v.SetVec(i, 1.0)
    }

    // Normalize
    norm := mat.Norm(v, 2)
    v.ScaleVec(1/norm, v)

    var lambda float64
    for iter := 0; iter < maxIter; iter++ {
        // Compute Av
        var Av mat.VecDense
        Av.MulVec(A, v)

        // Compute eigenvalue estimate
        lambdaNew := mat.Dot(&Av, v)

        // Normalize
        norm := mat.Norm(&Av, 2)
        Av.ScaleVec(1/norm, &Av)

        // Check convergence
        if iter > 0 && abs(lambdaNew-lambda) < tol {
            return lambdaNew, &Av
        }

        lambda = lambdaNew
        v.CopyVec(&Av)
    }

    return lambda, v
}

func abs(x float64) float64 {
    if x < 0 {
        return -x
    }
    return x
}

Benchmarking vs Python

func benchmarkEigen() {
    sizes := []int{50, 100, 200, 500}

    for _, n := range sizes {
        // Generate random symmetric matrix
        data := make([]float64, n*n)
        for i := 0; i < n; i++ {
            for j := i; j < n; j++ {
                val := float64((i+j)%17) - 8
                data[i*n+j] = val
                data[j*n+i] = val
            }
        }
        A := mat.NewSymDense(n, data)

        start := time.Now()
        var eig mat.EigenSym
        eig.Factorize(A, true)
        elapsed := time.Since(start)

        fmt.Printf("Size %4d: %v\n", n, elapsed)
    }
}

Summary

This article covered:

General eigendecomposition with mat.Eigen
Symmetric eigendecomposition with mat.EigenSym
Verifying eigenproperties
Power iteration for dominant eigenvalue
Performance benchmarking

Resources

Linear Algebra: Golang Series - View all articles in this series.

Note: This blog is a collection of personal notes. Making them public encourages me to think beyond the limited scope of the current problem I'm trying to solve or concept I'm implementing, and hopefully provides something useful to my team and others.

This blog post, titled: "Linear Algebra in Go: Eigenvalue Problems: Linear Algebra in Go Part 4" by Craig Johnston, is licensed under a Creative Commons Attribution 4.0 International License.